
Messen in der Chemie
3. Vorlesung
Praktisch jeder moderne Messaufbau in der Physikalischen Chemie ist computergestützt (im PC-Praktikum gibt es hiervon Ausnahmen, aber das sind dann keine zeitgemäßen Versuchsaufbauten, vielmehr dienen sie didaktischen Zwecken). Rechner spielen eine zentrale Rolle in verschiedenen Phasen (Abschnitten) eines Experimentes:
Curve Fitting, das spielt eine wichtige Rolle im PC-Praktikum).
Datenanalyse-Software enthält oft umfangreiche Mathematik-Pakete, die eine Auswertung der Messdaten überhaupt erst ermöglichen (Beispiel: Fourier-Transformation von Interferogrammen in der FTIR-Spektroskopie).
Neben Datenanalyse-Programmen gibt es auch reine Mathematik-Programme, die das Leben erheblich erleichtern, weil sie umständliche und fehleranfällige mathematische Prozeduren übernehmen, wie z.B. das Ableiten und Integrieren einer Funktion, oder das Auflösen einer Gleichung nach einer darin auftretenden Größe. Programme, die mit symbolischer Mathematik umgehen können, also z.B. das Ingetral \(\int x^2 \cdot \exp(-x) \diff x\) ausrechnen, oder den Grenzwert von \(\frac{\sin x}{x^2} \) an der Stelle \(x=0\) ermitteln können, werden CAS-Programme (CAS = Computer Algebra System) genannt.
Kommerzielle CAS-Programme können sehr viel Geld kosten. Es gibt aber einige kostenfreie Möglichkeiten, Mathematik am Computer zu betreiben, wenn man es nicht hauptberuflich tut; hier werden nur zwei aufgelistet.
Basic Accountzulegen, erhöht sich die Ihnen täglich zur Verfügung stehende Prozessorzeit.
Für unsere Zwecke sind Numerik-Programme aber viel wichtiger als CAS-Programme. Diese liefern nicht symbolische Lösungen eines Problems, sondern Zahlenwerte, beispielsweise die Fläche unter einer experimentell bestimmten Kurve.
Speziell zur zahlenmäßigen Flächenbestimmung gab es früher die Methode der Chemiker-Integration
: die auf Papier aufgetragene Kurve wurde bis zur Abszisse mit der Schere ausgeschnitten und auf eine Analysenwaage gelegt. Das ist heute nicht mehr zeitgemäß, da die Messdaten ohnehin digital vorliegen und dementsprechend mit einem Programm ausgewertet werden können.
Ein für unsere Zwecke fast immer geeignetes Programm zur Datenerfassung, -auswertung und -darstellung ist die Software Igor Pro des Herstellers WaveMetrics (Download Link), das zur Nutzung im Rahmen des Praktikums und begleitender Lehrveranstaltungen (also auch Messen in der Chemie
) allen Teilnehmern kostenlos zur Verfügung gestellt wird.
Im Folgenden werden wir mit Igor auf Tuchfühlung gehen; im weiteren Verlauf dieser Lehrveranstaltung werden wir es häufig nutzen.
Mittelwert, Varianz, Standardabweichung.
Wiederholte Messungen liefern nicht stets dasselbe Ergebnis. Beispiel: Wir setzen eine Lösung an, die nach einer bestimmten Zeit einem plötzlichen Farbumschlag unterworfen sein soll. Wird dieser Versuch einige Male wiederholt, so unterscheiden sich die Versuchsbedingungen doch jedes Mal geringfügig: die Konzentration der Lösung ist nicht dieselbe, die Temperatur kann geringfügig höher sein, die Helligkeit im Labor ist nicht dieselbe, die Adaptierung der Augen ist etwas anders als zuvor usw. Diese und ähnliche Änderungen in den äußeren Umständen führen zu zufälligen Schwankungen der gemessenen Zeit bis zur Wahrnehmung des Farbumschlags.Aus den Beobachtungen werden Messwerte gewonnen; diese bilden zunächst eine Reihe von Zahlenwerten.
Hier ist ein Beispiel einer solchen Messreihe:
6,86; 6,85; 7,39; 6,98; 8,02; 7,62; 6,30; 6,80; 7,03; 7,80; 7,2; 8,19
Die Messreihe ist eine Liste von Zahlenwerten (die zugeordnete Einheit ist hier ganz belanglos, es könnten also z.B. titrierte Milliliter sein). Für den \( i \)-ten Messwert wollen wir das Symbol \( x_{i} \) verwenden.
Der wichtigste Informationsgehalt einer Messreihe, bei der wiederholt dieselbe Größe gemessen wird, ist ihr Mittelwert \( \mu \).
Es lässt sich theoretisch zeigen, dass der Mittelwert \(\mu\) mit größerer Wahrscheinlichkeit dem wahren Wert entspricht als irgendeiner der Einzelwerte.
In vielen Fällen gibt es aber in der Realität nichts, was einem wahren Wert
entsprechen könnte. Beispiel: wenn wir das Körpergewicht aller Teilnehmer an dieser Lehrveranstaltung messen, entsteht eine Liste aus Zahlenwerten, aber dem Mittelwert entspricht nicht eine reale Person.
Wir haben also insgesamt \(N\) Messpunkte; wir summieren alle Messwerte \(x_i\), also \(x_1\), \(x_2\), \(x_3\) und so weiter, und teilen diese Summe durch die Anzahl \(N\) der Messungen. Unter das Summenzeichen \(\sum\) schreibt man den Startwert der Laufzahl \(i\), also den Index des ersten Messwerts \(x_1\), und über das Summenzeichen die Laufzahl des letzten der \(N\) Messwerte, also \(N\). Der Einfachheit halber lässt man bei der Obergrenze das \(i=\)
gewöhnlich weg und schreibt einfach \(N\), wenn das eindeutig ist. So wollen wir auch im Folgenden verfahren.
Der Mittelwert ist auf den meisten wissenschaftlichen Taschenrechnern als
Funktion vorhanden, das Zeichen dafür ist häufig \( \mu \) oder \( \bar{x} \) (lies: x quer
). Machen Sie sich bitte mit der entsprechenden Funktionalität Ihres Taschenrechners anhand der Betriebsanweisung vertraut.
Eine Liste kann in Igor importiert werden. Eine Liste wird in Igor als Wave repräsentiert, denn eine Wave ist ja zunächst nichts weiter als eine Liste von Zahlenwerten.
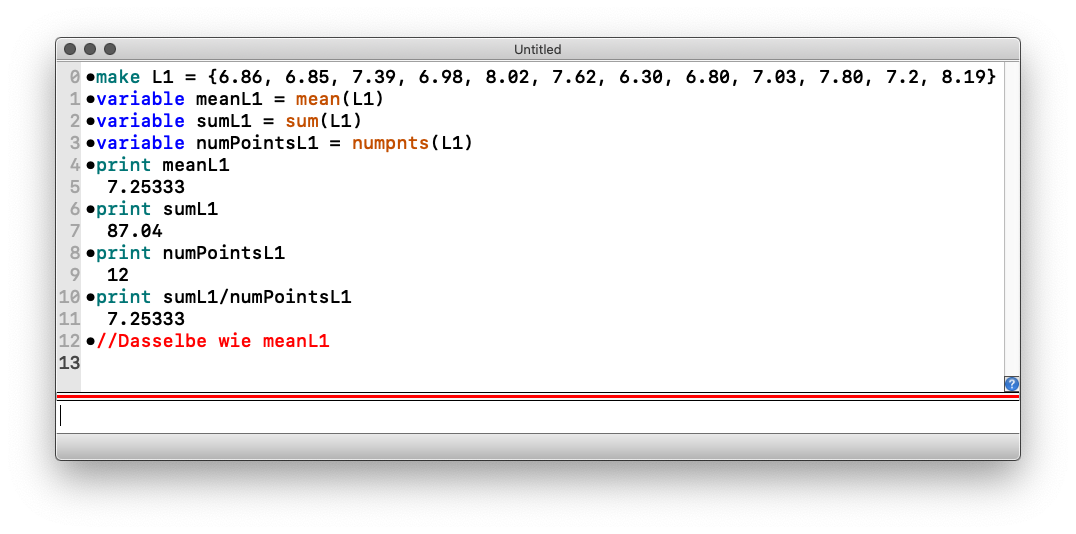
Damit wir mit der Liste in Igor bequem arbeiten können, definieren wir sie und geben ihr einen Namen, zum Beispiel L1. Geben Sie also bitte an der nächsten Befehlszeile ein (copy-paste funktioniert):
pasten. Die Werte müssen dann aber durch ein Zeilenende-Zeichen voneinander separiert sein, nicht durch Kommata.
sprechenzu lassen, also die Daten direkt aus einem Messgerät über eine geeignete Schnittstelle (z.B. RS-232) in Igor einzulesen.
Bitte beachten Sie:
Die Wave L1 ist jetzt definiert. Igor verfügt über Funktionen, die auf die Liste wirken.
Damit sind wir mit der Bestimmung des Mittelwertes auch schon fertig. In der Abbildung 3-1 sehen Sie Ein- und Ausgabe im Kommandofenster:

Streuung um den Mittelwert.– Neben dem Mittelwert interessiert uns die Frage, in welchem Ausmaß die Einzelwerte um dieses Mittel schwanken, oder, wie wir lieber sagen, streuen. Wir wollen ja wissen, wie nahe unsere Einzelwerte beim Mittelwert liegen.
Man könnte vielleicht zunächst geneigt sein, analog zur Mittelwertbildung die Schwankung der Werte durch den Mittelwert der Abweichung \(x_i-\mu\) der Einzelwerte vom Mittelwert \(\mu\) der Liste zu definieren, also den Ausdruck \[ \frac{1}{N} \cdot \sum_{i=1}^{N} \left(x_{i}- \mu\right) \] zu verwenden, aber man überzeugt sich leicht, dass dieser Ausdruck stets Null ergibt (das liegt daran, dass die positiven und negativen Abweichungen der Einzelwerte vom Mittelwert sich immer genau kompensieren, probieren Sie es ruhig mit der Liste L1 aus!). Das funktioniert also prinzipiell nicht.
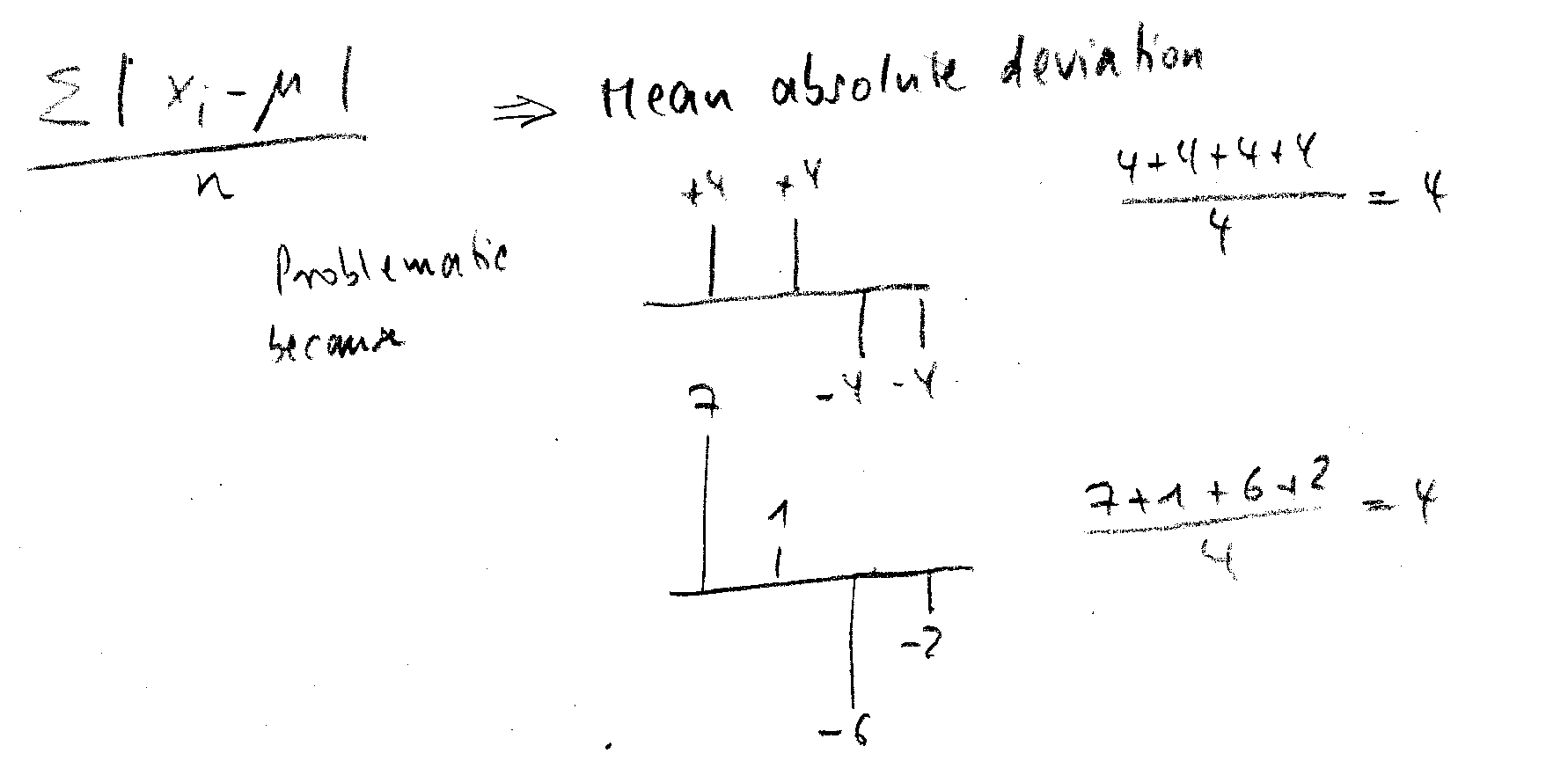
Um die gegenseitige Kompensation der Abweichungen vom Mittelwert zu eliminieren, könnte der Ausdruck \[ \frac{1}{N} \sum_{i=1}^{N} \left|{x_{i}- \mu}\right| \] verwendet werden (also unter Nutzung der Beträge der Abweichungen); aber auch dieser schafft Probleme. Dies ist in der Abb. 3-2 gezeigt.
Als Maß der Streuung wird häufig die Varianz \( V \) verwendet. Sie ist wie folgt definiert: \begin{equation} \label{eqDefVariance} V = \frac{1}{N} \cdot \sum_{i=1}^{N} \left(x_{i} - \mu \right)^{2.} \end{equation} Beachten Sie das Quadrat in der Summe. Wir summieren also die Quadrate der Abweichungen.
Auch bei der Varianz als Maß der Steubreite treten Probleme auf:
Im PC-Praktikum, und generell in der Physikalischen Chemie, wie die Standardabweichung \( \sigma \) als Maß der Streuung der Einzelwerte verwendet. \(\sigma\) ist definiert als die Quadratwurzel aus der Varianz: \begin{equation} \label{eqDefStdDev} \sigma = \sqrt{V} = \sqrt{ \frac{1}{N} \cdot \sum_{i=1}^{N} \left(x_{i} - \mu \right)^{2} } \end{equation}
Die in Gl. \ref{eqDefStdDev} definierte Größe \( \sigma \) wird auch als Gesamtstandardabweichung bezeichnet. Man muss tiefer in die Urgründe der Statistik einsteigen, um den Hintergrund dieses Begriffes zu verstehen.
Neben dieser Gesamtstandardabweichung \(\sigma\) wird die Probenstandardabweichung \( \sigma_{P} \) verwendet; diese ist definiert als \begin{equation} \label{eqProbenstandardabweichung} \sigma_{P} =\sqrt{ \frac{1}{N-1} \cdot \sum_{i=1}^{N} \left(x_{i} - \mu \right)^{2} } \end{equation}
Sie unterscheidet sich von der in Gl. \ref{eqDefStdDev} definierten Gesamtstandardabweichung (die wir auch als Standardabweichung schlechthin bezeichnen) durch das Auftreten der Größe \(N-1\) statt \(N\) im Nenner vor dem Summenzeichen. Für große \(N\) ist der Unterschied irrelevant. Auf Taschenrechnern ist meist \( \sigma_{P} \) verfügbar (dies muss im Handbuch des Taschenrechners nachgelesen werden).Zur Gesamtstandardabweichung \( \sigma \) entsprechend Gl. \ref{eqDefStdDev} gelangt man, indem man in den Taschenrechner zunächst alle Werte in das Summenregister eingibt, dann den Mittelwert \(\mu\) berechnen lässt, diesen dann ebenfalls in das Summenregister eingibt und erst danach die Standardabweichung vom Taschenrechner mit der entsprechenden Befehlstaste errechnen lässt.
Der Unterschied zwischen der Standardabweichung der Gesamtheit \( \sigma \) und der Standardabweichung der Probe \( \sigma_{P} \) ist fast immer belanglos. Um Dinge nicht allzu kompliziert zu machen, können Sie in der Regel mit demjenigen \( \sigma \) rechnen, das Ihr Computerprogramm bzw. Taschenrechner anbietet, außer es wird ausdrücklich Wert auf den Unterschied gelegt.
Mit der Software Igor können Sie die Standardabweichung der Werte aus der Liste L1 (siehe oben) erhalten. Es gibt aber (meines Wissens zumindest) keinen Befehl, der unmittelbar \(\sigma\) liefern würde. Statt dessen verwenden wir den Befehl wavestats, der eine Fülle von statistischen Informationen über den Datensatz liefert. Führen Sie also den folgenden Befehl aus:
Die Ausgabe sieht dann wie folgt aus:
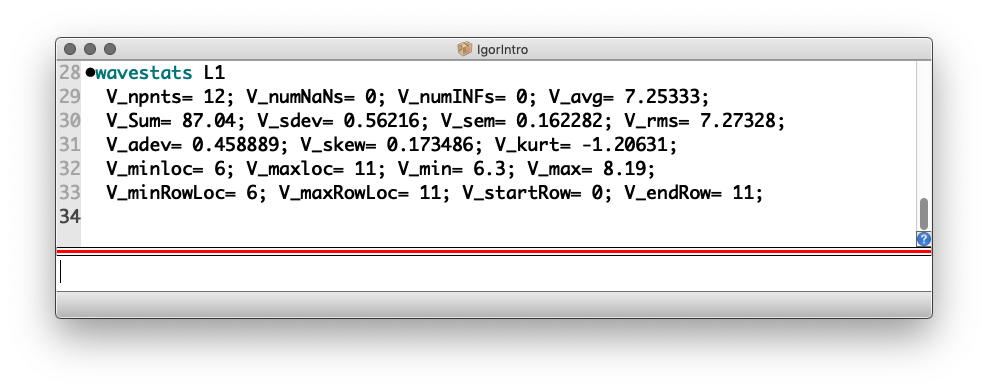
Hier die wichtigsten der erzeugten Variablen (sie beginnen alle mit V_
):
unendlichenthalten; für uns von geringer Bedeutung.
verbessert die Statistik, aber nur im folgenden Sinne:
Der Fehler des Mittelwertes ist nicht dasselbe wie die Standardabweichung. \(\sigma\), die Standardabweichung, gibt an, wie stark Messpunkte um einen Mittelwert streuen. Der Fehler des Mittelwertes, den wir mit \(\Delta \mu\) bezeichnen, gibt an, wie genau der Mittelwert \(\mu\) bekannt ist; wie groß seine Unsicherheit \(\Delta \mu\) ist. \(\Delta \mu\) hängt aber eng mit der Standardabweichung \(\sigma\) zusammen und ist definiert als \begin{equation} \label{eqErrorOfMean} \Delta \mu = \frac{\sigma}{\sqrt{N}}. \end{equation}
Probieren Sie es aus; geben Sie ein:
und Sie erhalten den Zahlenwert von \(\Delta \mu\).
Um den Fehler des Mittelwertes zu erhalten, teilen wir also die Standardabweichung \(\sigma\) nochmals durch die Wurzel aus der Zahl der Messdaten.
Gegeben sei eine Standardabweichung von \(\sigma=3.5\) bei einer Anzahl von 20 Datenpunkten. Der Fehler des Mittelwertes ist dann gegeben zu
\[ \Delta \mu_1 = \frac{3.5}{\sqrt{20}};\] wenn wir aber 40 Messpunkte aufnehmen, so erhalten wir: \[ \Delta \mu_2 = \frac{3.5}{\sqrt{40}}.\] Teilen wir die beiden \(\Delta \mu\)-Werte durcheinander, so finden wir: \[ \frac{\Delta \mu_1}{\Delta \mu_2} = \frac{3,5 \cdot \sqrt{40}}{\sqrt{20}\cdot 3,5} = \frac{\sqrt{40}}{\sqrt{20}} = \sqrt{\frac{40}{20}} = \sqrt{2}.\]Bei der halben Anzahl an Messpunkten (20 statt 40) ist also der Fehler des Mittelwertes \(\Delta \mu\) um den Faktor \(\sqrt{2}\) größer. Um einen zehnfach kleineren Fehler des Mittelwertes \(\Delta \mu\) zu erhalten, müssen wir die Anzahl an Messungen verhunderfachen.
Wenn Sie aus einer Messreihe den Mittelwert und den Fehler des Mittelwertes angeben wollen, so verwenden Sie für den Fehler des Mittelwertes bitte den Ausdruck in der Gl. \ref{eqErrorOfMean}.
Mittelwertbildung fehlerbehafteter Größen.–
Die bisherigen Gleichungen gehen davon aus, dass die Messwerte in statistischer Weise um einen Mittelwert schwanken, und es wurden die üblichen statistischen Methoden verwendet, um einen Mittelwert, die Standardabweichung und den Fehler des Mittelwertes zu ermitteln.Häufig kennen wir aber zusätzlich den individuellen Fehler \(\Delta x_i\) der Messwerte \(x_i\). Wir erhalten z.B. aus verschiedenen Messverfahren eine gewisse Größe mit unterschiedlichem Einzelfehler (es könnte sich z.B. um die Messung einer Naturkonstante mit unterschiedlichen Messmethoden handeln). Hierfür gibt es besondere Vorschriften, die wir hier nicht herleiten, sondern nur mitteilen.
Dabei gelten die folgenden Gleichungen:
Diese Gleichungen gelten auch für den wichtigen Sonderfall, dass alle Fehler \(\Delta x_i\) einander gleich sind.
In Worten: den Mittelwert fehlerbehafteter Größen bestimmen wir, indem wir jeden Messwert durch das Quadrat seines individuellen Fehlers teilen, daraus die Summe bilden, und diese Summe durch die Summe der Kehrwerte der Quadrate der individuellen Fehler teilen.
Die Gleichungen \(\ref{eqMittelwertFehlerbehaftet}\) und \(\ref{eqFehlerMittelwertFehlerbehaftet}\) sehen furchterregend aus, sie können aber mit Hilfe eines Tabellenkalkulationsprogrammes wie MS Excel oder auch mit Igor ohne viel Mühe genutzt werden.
Die Messdatenreihe weise die folgenden Elemente auf:
{6, 5.8, 6.3, 6.1, 5.9, 6.2, 6.1}
Die Fehler der Einzelmessungen seien wir folgt gegeben:
{0.2, 0.3, 0.2, 0.4, 0.1, 0.1, 0.2}
Wir führen hier vor, wie man \(\mu\) und \(\Delta \mu\) mit Microsoft Excel ermittelt.
Hier ist die Tabelle als Graphik gezeigt:
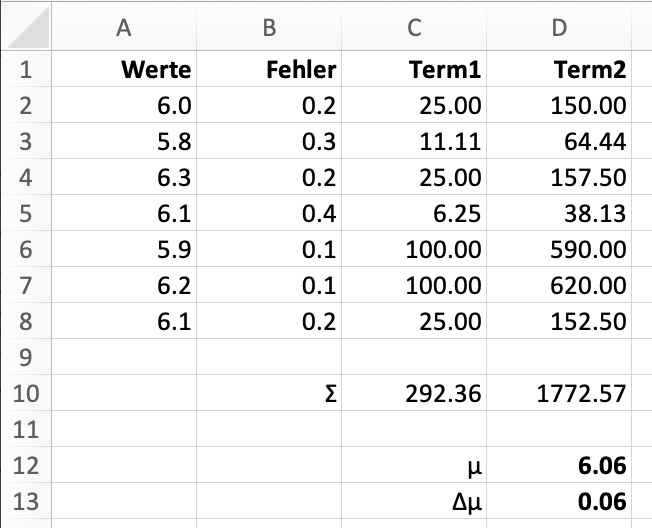
Die Spalten A und B enthalten die Werte und deren individuelle Fehler.
Die Spalte C (Term1
) enthält die \(\frac{1}{(\Delta x)^2}\). Der Wert 25.00
in Zelle C2 wird erzeugt durch Eingeben des Befehls:
=1/(B2*B2)
Die Werte in Spalte D (Term2
) entsprechen \(\frac{x}{(\Delta x)^2}\), sind also gleich dem Produkt aus A und C; der Befehl lautet:
=A2*C2
Für die Zeilen 3–8 brauchen Sie lediglich die Befehle aus der Zeile 2 in die Zeilen 3–8 zu kopieren.
Zelle C10 enthält \(\sum_{i=2}^{8}\frac{1}{\left(\Delta x_i\right)^{2}}\), also die Summe aus C2–C8:
=SUM(C2:C8)
D10 enthält \(\sum_{i=2}^{8}\frac{x_i}{\left(\Delta x_i\right)^{2}}\); der Excel-Befehl lautet:
=SUM(D2:D8)
Der Mittelwert \(\mu\) in Zelle D12 wird erhalten durch:
=SUM(D10:C10)
Den Fehler des Mittelwertes \(\Delta \mu\) in Zelle D13 erhält man durch die Eingabe
=SQRT(1/C10)
Damit ergibt sich der Mittelwert zu \[\mu = 6.06\] und der Fehler des Mittelwertes zu \[\Delta \mu = 0.06\]Wir wollen nun ein Computerspiel machen, das Ihnen einen Eindruck von den Ursachen der Streuung von Messdaten vermitteln kann. Das Spiel heißt Quincunx und zeigt die Verteilung von zufälligen Ereignissen. Hier ist der Link auf Quincunx. Klicken Sie bitte auf den Link, so dass sich ein weiteres Browserfenster öffnet und Sie das Spiel sehen.
So sieht die Spielfläche von Quincunx aus:
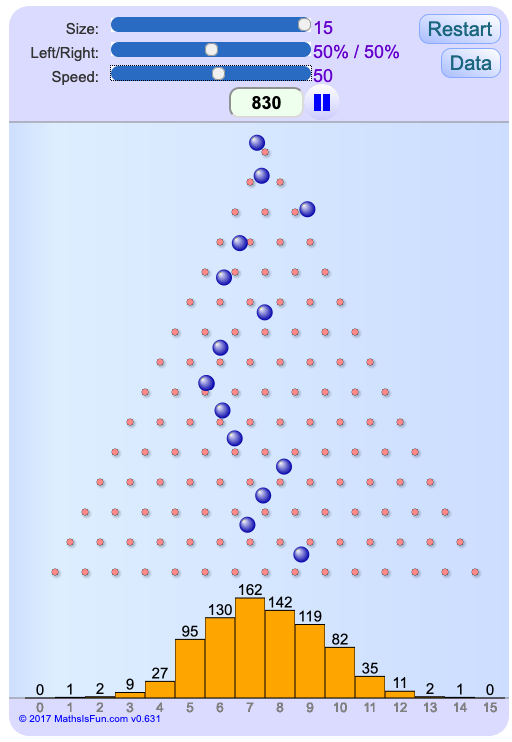
Stellen Sie bitte den Schieberegler Size
auf den Maximalwert (15) und Speed
auf 50. Klicken Sie dann Restart
.
Die blauen Bälle, die nach unten fallen, treffen auf Stangen (die Sie von vorne sehen). Die Wahrscheinlichkeit, dass ein Ball links an der Stange entlang fällt, ist gerade so groß, wie dass er rechts daran herabfällt. So hüpft jeder Ball beim Fallen immer zwischen Stangen hin und her. Unten im Bild sehen die die Häufigkeiten, mit denen die Bälle schließlich in den einzelnen Bereichen unter den Stangen auftreffen. Sie werden feststellen, dass die meisten Bälle nahe der Mitte des Feldes landen, aber eben nicht alle Bälle. Einige treffen auch weit entfernt von der Mitte auf. Da die Verteilung rein zufällig ist, werden Sie bei einer Wiederholung des Spieles während einer gleich langen Zeit nicht wieder genau dieselbe Verteilung erhalten, sondern nur eine ihr ähnliche.
Bitte lassen Sie nach Möglichkeit das Spiel über Nacht laufen. Im Laufe der Zeit wird die Verteilung der Bälle auf die zur Verfügung stehenden Plätze immer regelmäßiger. Dahinter steckt eine strenge Gesetzmäßigkeit, die man Binomialverteilung nennt.
Abbildung 3-6 zeigt ein Beispiel:
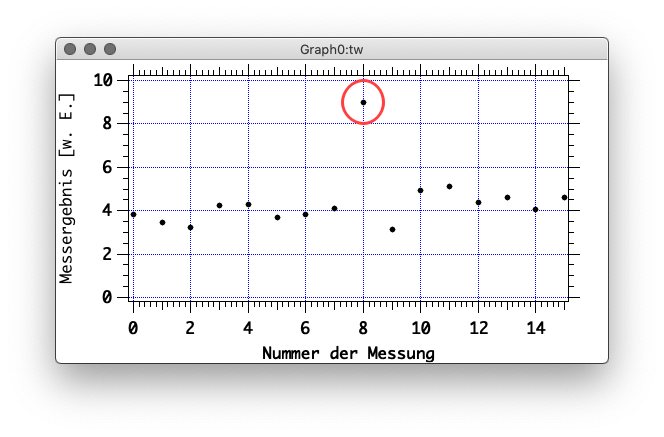
Ausreißer
oder sollte er bei der Mittelwertbildung berücksichtigt
werden?
Hier sind die Messdaten mit der Anweisung, daraus eine Igor-Wave zu machen (das Nachfolgende ist also in die Igor-Kommandozeile zu übertragen):
make tw = {3.81599, 3.4633, 3.2439, 4.23815, 4.28283, 3.70816, 3.81192, 4.0863, 9.0238, 3.14665, 4.94752, 5.09755, 4.3839, 4.62207, 4.0626, 4.5942}
Sie können die Werte auch in eine Tabelle übertragen, die Sie an der Kommandozeile mit dem Befehl edit erzeugt haben.
Wie man aus den Daten der Wave tw eine geeignete Graphik erzeugt, steht hier.
Wenn Sie den weiter oben erklärten Befehl wavestats auf tw anwenden, so erhalten Sie:
V_avg = 4.40805; V_sdev = 1.35289,
also \(\mu \approx 4,4\) und \(\sigma_{P}= 1,4 \).
Bitte ersetzen Sie jetzt Messpunkt 8 (der rot umrundete; beachten Sie, dass Igor beim Zählen mit Null beginnt, es ist der neunte Messpunkt) durch NaN (not a number
, das bedeutet, dass der Inhalt des Punktes keine Zahl ist und daher bei Auswertungen nicht mitgenommen
wird), indem Sie die Nummer des Messpunktes in eckigen Klammern hinter den Namen der Wave setzen:
… und jetzt wenden Sie nochmals wavestats darauf an; Ergebnis:
V_avg = 4.10034; V_sdev = 0.581209,
also \(\mu \approx 4,1\) und \(\sigma_{P} \approx 0,6 \).
Das ist schon ein Unterschied! Der Mittelwert ist von 4,4 auf 4,1 abgesunken, und die Standardabweichung hat um mehr als 50% abgenommen. Aber Punkt 8 ist ein Messpunkt wie jeder andere. Inwiefern sind wir überhaupt berechtigt, eine Messpunkt wegzulassen?
In den labororientierten Naturwissenschaften kommen Ausreißer ständig vor. Durch eine elektrische Störung kann ein Detektor beispielsweise ein Signal produzieren, das offensichtlich viel zu intensiv ist, um echt
zu sein. Bei Messungen mit Synchrotronstrahlung in Adlershof hat zum Beispiel früher die nahe gelegene S-Bahn gestört. Wir haben also häufig Veranlassung, falsche Datenpunkte zu unterdrücken. Die kritische Begutachtung von Datenpunkten gehört zur professionellen Routine experimentell orientierter Naturwissenschaftler.
Anhand des Quincunx-Spieles konnten Sie sich davon überzeugen, dass Ergebnisse um einen Mittelwert streuen können. Die einzelnen Datenpunkte (in Quincuncx: die Position der Bälle) treten mit unterschiedlicher Häufigkeit auf. Die Verteilung gehorcht strengen Gesetzmäßigkeiten, die umso deutlicher zu Tage treten, je mehr Ereignisse beobachtet werden.
Wir können die Häufigkeit des Auftretens eines bestimmten Ereignisses dadurch erfassen, dass wir die Ereignisse in ein Histogramm einsortieren. Ein Histogramm sortiert Ereignisse nach der Häufigkeit ihres Auftretens.
Das Spiel Quincunx liefert unmittelbar ein Histogramm. Normalerweise muss man das Histogramm aber aus den Daten selbst erstellen.
Die Verteilung, die sich beim Spielen von Quincunx einstellt wird auch als Normalverteilung bezeichnet.
In der ersten Abbildung sehen Sie links eine mit Igor Pro erzeugte Normalverteilung von 128 Datenpunkten, die um den Schwerpunkt 5 streuen. (Es handelt sich um Zeiten bis zum Auftreten eines Ereignisses, aber das ist hier nicht wichtig.) Auf der rechten Seite der Abbildung sehen Sie das zugehörige Histogramm, das Ereignisse summiert, die jeweils innerhalb derselben Sekunde aufgetreten sind. Beispielsweise sind 35 Ereignisse nach 4 bis 5 Sekunden aufgetreten, und 10 Ereignisse nach 3 bis vier Sekunden. Die Intervallbreite beträgt also jeweils 1 Sekunde. Die Verteilung erinnert sehr stark an die Verteilung von Bällen im Quincunx-Spiel.
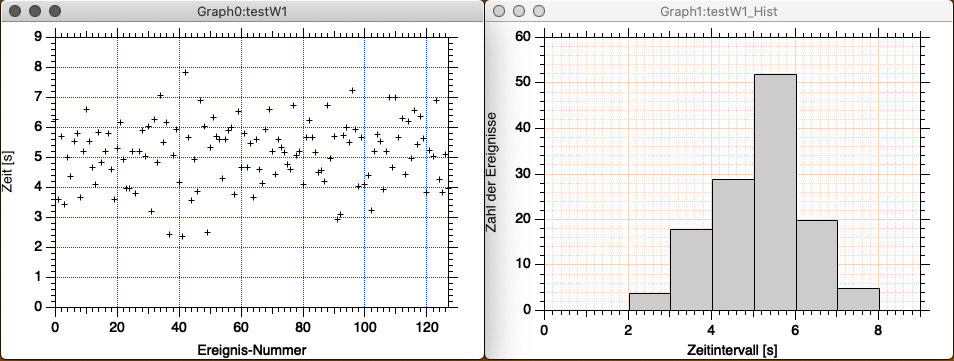
Wir konstruieren das jetzt gemeinsam mit Igor:
.5ist eine gang und gäbe Abkürzung für
0.5.
Das sollte ein Bild ähnlich dem in Abb. 3-7 ergeben, wenn Sie entsprechend der verlinkten Anleitung zum Erstellen von Graphiken die Voreinstellungen entsprechend gesetzt haben. Das Entscheidende hier ist die Funktion gnoise(). Der Befehl testW1 = 5 + gnoise(.5) schreibt die Zahl \(5\) in jedes der 128 Elemente der Wave, und addiert zusätzlich in jedes Element die Ausgabe des Befehls gnoise(0.5). Das ist kurz gesagt eine Verrauschungsfunktion, das Argument in Klammern gibt das Ausmaß der Verrauschung an. Wir werden gnoise später noch genauer kennenlernen; hier sei aber schon gesagt, dass gnoise einen speziellen Grenzfall der Normalverteilung liefert, die wir auch bei Quincunx kennengelernt haben.
Wenn wir den Befehl testW1 = 5 + gnoise(.5) erneut aufrufen, erhalten wir eine neue Zufallsverteilung. Zum erneuten Aufrufen brauchen wir den Befehl nicht nochmals manuell einzugeben; wir klicken einfach auf den Befehl in der History und bestätigen mit der Return-Taste, dann wir der Befehl in die Kommandozeile kopiert. Probieren Sie es bitte mehrfach aus, andere Verteilungen zu erzeugen, damit Sie ein Gefühl dafür bekommen. Da gnoise eine Zufallsverteilung erzeugt, wird das Resultat jedesmal ein wenig anders aussehen.
Wir erzeugen jetzt mit Igor das entsprechende Histogramm, wir sortieren die Ereignisse also in Bereiche (Intervalle, bins
), innerhalb deren sie auftreten. Wir klicken im Menü Analysis
auf Histogram…
, es öffnet sich eine Dialogbox. Wir übernehmen die Einstellungen aus der Abbildung:
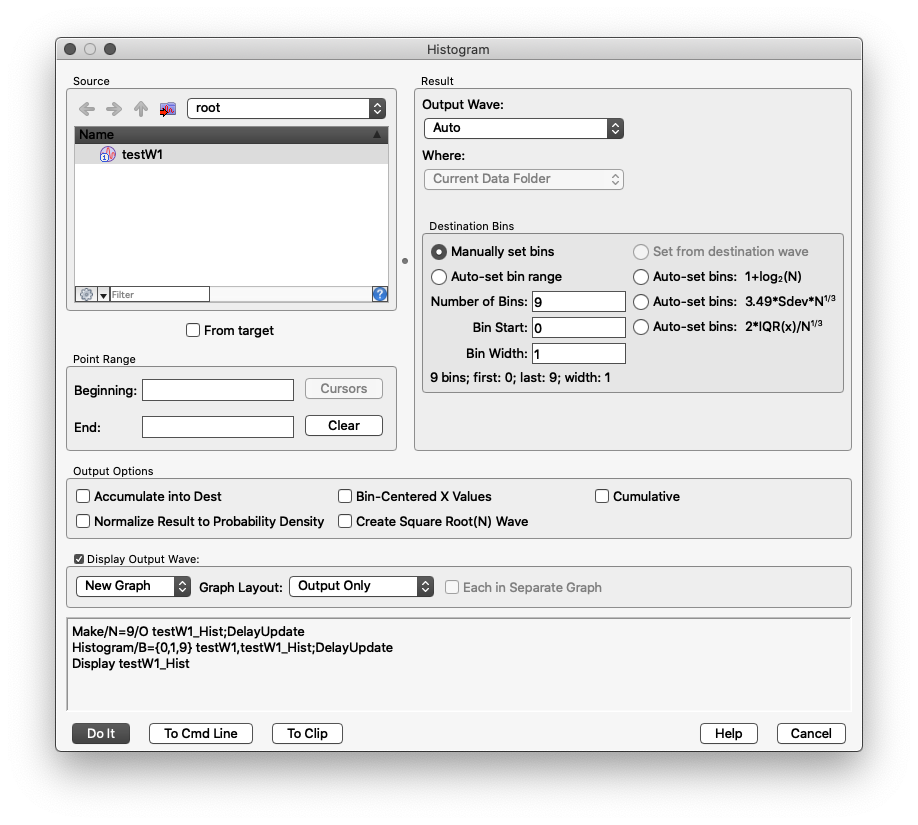
Number of Bins
, Bin Start
und Bin Width
. Beachten Sie, dass im unteren Bereich des Fensters die Kommandozeilen-Befehle notiert sind, die beim Klicken auf Do it
ausgeführt werden. Die entscheidende Zeile lautet: Histogram/B={0,1,9} testW1,testW1_Hist.
Die Bedeutung der Zahlen ist:
Histogram/B={start,binbreite,Anzahl bins} testW1,testW1_Hist.
Beim Ausführen des Befehls werden diese Zeilen in die History kopiert, so dass wir darauf Zugriff haben, ohne jedesmal die Dialogbox öffnen zu müssen.
Doppelklicken Sie in der graphischen Darstellung des Histogramms auf testW1_Hist und übernehmen Sie die Einstellungen aus der folgenden Dialogbox:
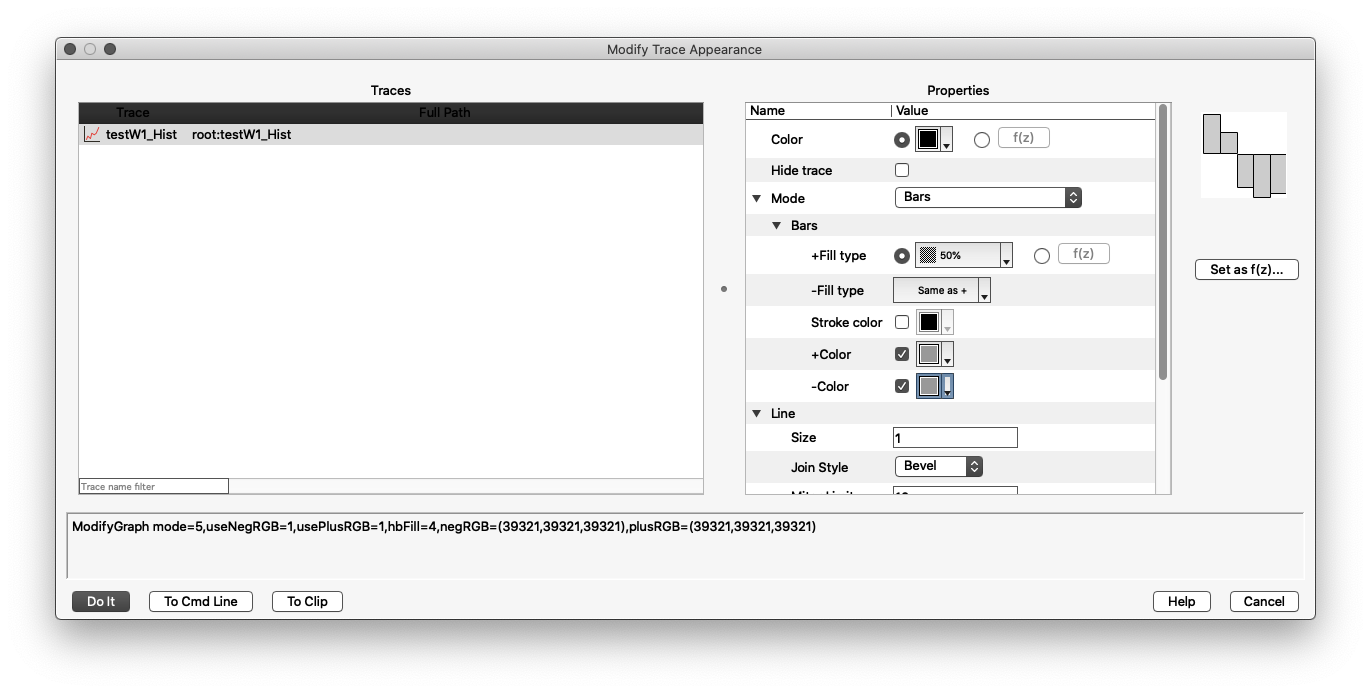
text-align:left;ModifyGraph mode=5,useNegRGB=1,usePlusRGB=1,hbFill=4,negRGB=(39321,39321,39321),plusRGB=(39321,39321,39321)
Unser Histogramm zeigt beispielsweise, dass 5 Ereignisse in das Zeitintervall zwischen 7 und 8 Sekunden fallen. (Zählen Sie nach!)
Die Abbildung 3-10 zeigt links dieselben Ereignisse wie in Abb. 3-7, und rechts die Sortierung in ein Histogramm, dessen Intervallbreite nur 0,125 Sekunden beträgt.
Wir können es aus dem bisherigen Histogramm wie folgt leicht mit folgendem Befehl erzeugen:
Da die Intervallbreite jetzt nur noch 0.125 beträgt, also 1/8 der bisherigen, brauchen wir 8 mal so viele Bins, daher 56.
Es fällt sofort auf, dass das Histogramm nun weniger regulär und glatt erscheint. Die Ursache ist leicht zu verstehen: da unsere Intervallbreite nur 0,125 s beträgt, enthält das Intervall 8 mal mehr Kanäle zum Verteilen der Ereignisse. Bei gleichbleibender Anzahl von Ereignissen ist die Verteilung noch nicht so ausgeprägt durch die Verteilungsgesetze gesteuert. Sie ist daher ruppiger
, weniger glatt:
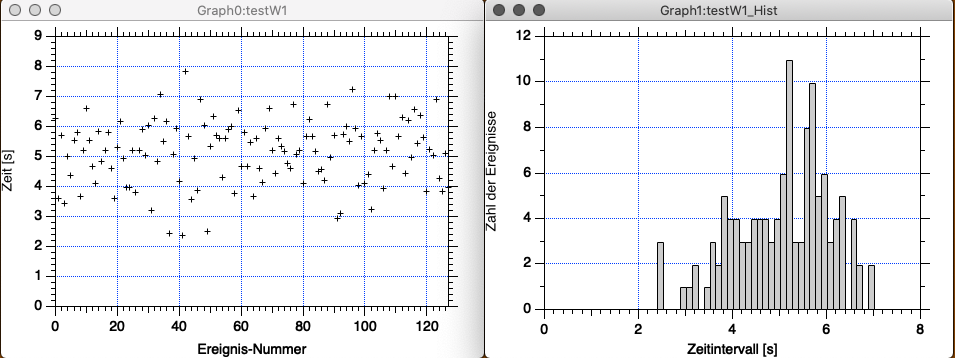
Die Abbildung 3-11 zeigt wiederum normalverteilte Ereignisse und das Histogramm; die Intervallbreite des Histogramms ist wiederum 0,125 s, gerade so wie in der Abb. 2; aber die Zahl der Ereignisse beträgt nun 1024, und nicht mehr, wie bisher, 128 Ereignisse (in der Programmiererei wählt man als Punktzahl gerne Potenzen von 2).
Mit Igor ganz einfach zu erzeugen:
/oüberschreibt die bisherige Wave testW1 mit 1024 Punkten. Sie erkennen, dass die Erhöhung der Zahl der Ereignisse nun weniger irregulär erscheint. Die Häufung um 5 herum ist viel deutlicher zu erkennen.
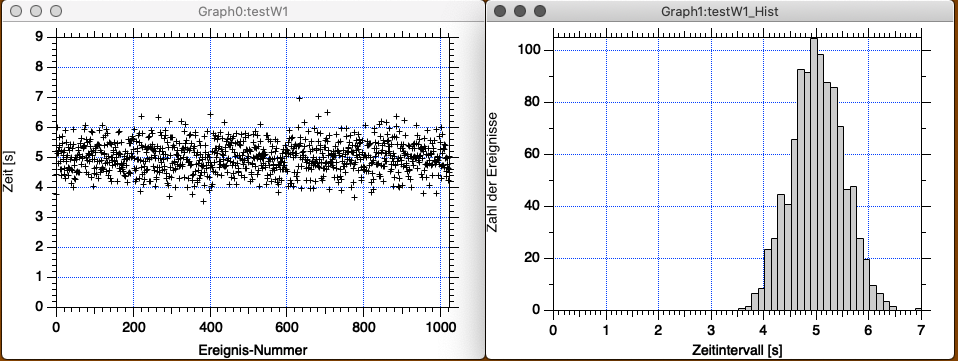
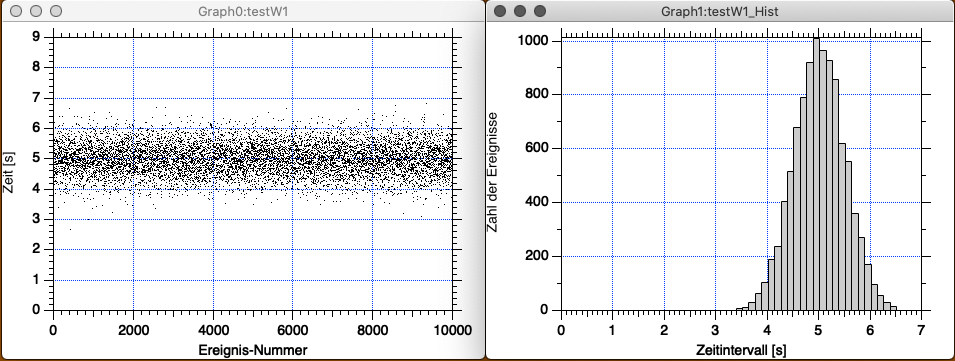
In der nun folgenden Abb. 3-12 sehen Sie links \(10^{4}\) normalverteilte Ereignisse und ein Histogramm mit einer Intervallbreite von \(0,125\;{\rm s}\) je Kanal:
Dotsund nicht als Marker dargestellt (siehe Igor-Dialogbox
Modify Trace Appearance). Die im Histogramm Abb. 3-12 (rechts) dargestellte Verteilung ist nochmals regulärer und glatter (vgl. Abb. 3-11 rechts).
Die nächsten Abbildungen zeigt die Ergebnisse für 1 Million Ereignisse. Die Kommandos für Igor sind wie zuvor, lediglich müssen Sie make/o/N=(10^6) testW1 schreiben, statt N=(10^4). Igor berechnet dann eine Million mal (!) den Wert 5 + gnoise(0.5) (man merkt, dass es einen kleinen Moment dauert), siehe Abb. 3-13; wie wir sehen, wird das Histogramm sehr symmetrisch und glatt:
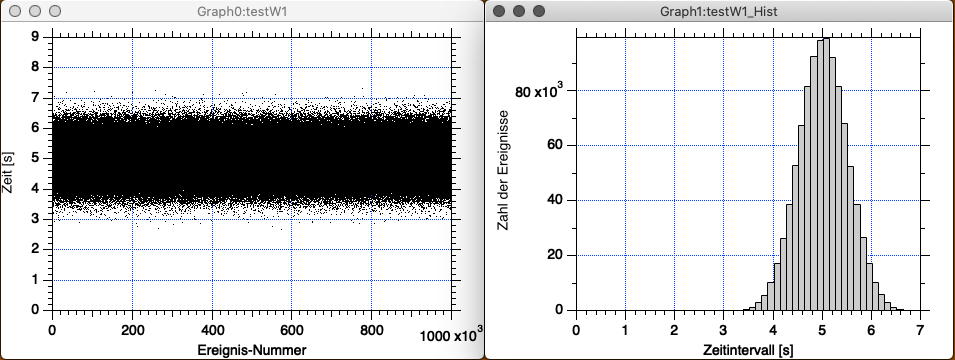
Und jetzt machen wir noch 10 Millionen Ereignisse und verschmälern die Bin-Breite um den Faktor zehn (und erhöhen die Anzahl der Bins um den Faktor zehn):
Wir stellen fest, dass Igor jetzt wirklich einige Zeit benötigt, um die Wave testW1 zu erzeugen (hängt von der Rechenleistung unseres Computers ab, hier dauerte es einige Sekunden). Die Datenpunkte erscheinen als ein schwarzes, am Rand ausgefranstes Band. Zur graphischen Darstellung des Resultats für das Histogramm haben wir in Modify Trace Appearance
den Punkt Line between Points
gewählt, um nur die Einhüllende zu zeigen, vgl. Abb. 3-14:
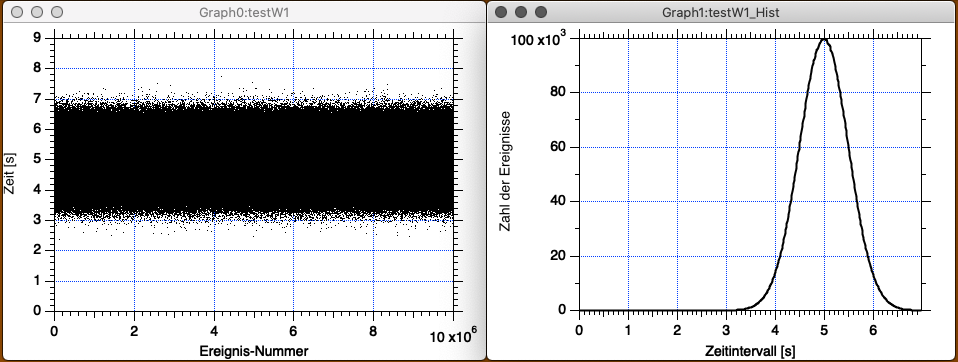
Die Gestalt der Einhüllenden des Histogramms in Abb. 3-14 erinnert uns an die bekannte Gausssche Glockenkurve. Und das ist kein Zufall. Wir werden gleich sehen, warum.
Igor-Info: Skalieren einer Igor-Wave.-Bevor wir inhaltlich weitermachen, wollen wir noch eine weitere Eigenschaft von Igor-Waves kennenlernen: die Skalierung.
Wie Sie wahrscheinlich wissen, können elektronische Dateien sowohl Daten als auch Metadaten enthalten. So enthält eine mp3-Musik-Datei nicht nur die Musik (das sind die Daten), sondern beispielsweise auch den Namen des Komponisten, den Namen des Albums, auf dem der Musiktitel erscheint, den Namen des Stückes u.s.w. In einem Musik-Abspielprogramm können Sie alle diese Daten dann sehen. Man bezeichnet diese Dinge als Metadaten, weil sie zusätzlich zu den eigentlichen Daten gespeichert sind.
Auch Igor-Waves können Metadaten zugeordnet werden. Beispielsweise kann man in eine Wave einen zusätzlichen Textkommentar hineinschreiben (aber wir werden hier nicht lernen, wie das funktioniert).
Unter der Skalierung einer Wave versteht man die Zuordnung eines x-Wertebereiches, auf den sich die Daten der Wave beziehen. Der erste Datenpunkt der Wave bezieht sich dann auf den x-Startwert, und der letzte Datenpunkt auf den letzten x-Wert. Wir wollen hierzu ein Beispiel betrachten. Bitte geben Sie ein:
Sie sollten ungefähr folgende Abbildung erhalten:
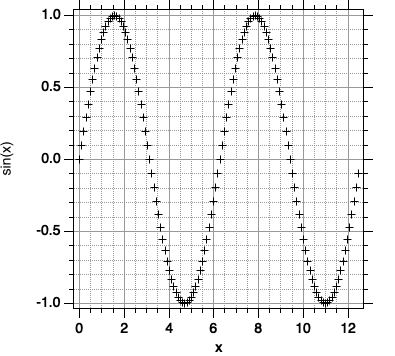
Wir können sinWave nachträglich umskalieren und den Sinus der x-Werte erneut ausrechnen lassen:
Ergebnis:
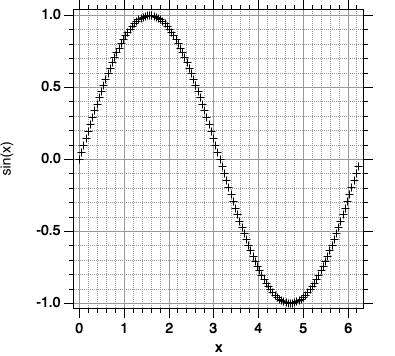
Wenn Sie keine Skalierung vornehmen, stellt Igor die Daten der Wave über Punktnummer dar.
Wenn wir den Wert für ein bestimmtes \(x\) innerhalb des durch setscale definierten Wertebereiches abfragen wollen (z.B. an der Stelle \(x=2.3\), dann geben wir ein:
Eckige Klammern hinter dem Namen der Wave, also zum Beispiel myWave[121], beziehen sich auf die Punktnummer; runde Klammern (myWave(6.5)) auf einen x-Wert.
Statt den Befehl setscale an der Kommandozeile einzugeben, können wir auch im Menü Data
den Befehl Change Wave Scaling…
aufrufen. Es erscheint eine Dialogbox, die verschiedene Methoden der Skalierung erlaubt.
Wir können Igor also zur graphischen Darstellung von Funktionen nutzen. Davon wollen wir im Folgenden Gebrauch machen.
5.3— Wahrscheinlichkeiten.–Von den insgesamt \(N\) Ereignissen befinden sich \(\Delta N_{i}\) im i-ten
Intervall (in Igor Bin
genannt) des Histogramms. Wir nehmen an, es gebe insgesamt \(k\) Intervalle im Histogramm (zum Beispiel gibt es im Histogramm der Abb. 3-10 insgesamt 56 Intervalle, also ist \(k=56\). Die Summe der Inhalte aller Intervalle ist gleich der Gesamtzahl der
Ereignisse:
\begin{equation} \label{eqhistSum1}
\sum_{i=1}^{i=k} \Delta N_{i} = N.
\end{equation}
Gleichung \ref{eqhistSum1} können wir natürlich auch durch Umstellen wie folgt schreiben:
\begin{equation} \label{eqhistSum2} \frac{1}{N }\sum_{i=1}^{i=k} {\Delta N_{i}} = 1. \end{equation}Teilen wir also die Ordinate (die \(y\)-Achse) des Histograms durch die Gesamtzahl \(N\) der Ereignisse, so repräsentieren die einzelnen Balken, geteilt durch die Gesamtzahl der Ereignisse, also \(\frac{1}{N} \cdot \Delta N_i\) näherungsweise die Wahrscheinlichkeit \(\Delta W\), dass ein Ereignis in das entsprechende Intervall fällt. Die Summe dieser Wahrscheinlichkeiten muss gleich Eins sein, denn zu irgendeinem Zeitpunkt muss das Ereignis eintreten.
Wenn wir die Intervallbreite \(\Delta t\) (allgemein \(\Delta x\)) immer
kleiner machen, gelangen wir als Grenzwert zu einer infinitesimalen Breite
\(\diff t\) bzw. allgemein für eine Variable \(x\) zu einer infinitesimalen
Intervallbreite \(\diff x\) (ein unendlich schmales
Intervall). Ein unendlich schmales Intervall (Breite = Null)
\(\diff x\) um den Ort \(x_{0}\)
herum ist aber nichts anderes als die Zahl \(x_{0} \)
(wir erinnern uns daran, dass wir reelle Zahlen durch eine Intervallschachtelung erzeugen,
wenn wir zu einem infinitesimal schmalen Intervall gelangen). Aus dem
Histogramm wird damit eine stetige Funktion, die als Gausssche
Verteilungsfunktion (Gauss-Funktion, Glockenkurve, Dichtefunktion) bekannt ist. Die Gausssche Verteilungsfunktion ist eine stetige Funktion und der idealisierte Grenzfall eines Histogramms.
5.4— Die Gausssche Verteilungsfunktion.–
Als Grenzfall der soeben besprochenen Histogramme für den Fall \(\Delta x \to 0 \) stellt sich die Gausssche Verteilungsfunktion ein. Sie hat folgende Form (bitte nicht erschrecken, wir werden dies gleich gaaanz ausführlich erläutern): \begin{equation} \label{eqGaussFunc} g(x) = \frac{1}{\sigma} \cdot \sqrt{\frac{1}{2 \pi}} \cdot \exp \left( - \frac{1}{2} \frac{\left(x - \mu \right)^{2} }{\sigma^{2}} \right) \end{equation} Hierin ist: \(\mu\) der Schwerpunkt der Funktion (Ort des Maximums); \(\sigma\): ein Maß für die Breite der Glockenkurve, identisch mit der uns bereits bekannten Standardabweichung. Im Abstand \(\sigma\) vom Maximum \(\mu\) ist der Betrag der Steigung \(\diff{g(x)}{\diff x}\) der Gaussfunktion maximal (Wendestellen).Eine graphische Darstellung der Gauss-Funktion können wir mit Igor erzeugen. Wir wollen der Einfachheit halber zunächst \(\sigma = 1\) und \(\mu=0\) setzen. Die Funktion hat dann folgende Gestalt:
\begin{equation} \label{eqGaussFuncStart} g(x) = \sqrt{\frac{1}{2 \pi}} \cdot \exp \left( - \frac{1}{2} x^2 \right) \end{equation}In Igor:
Sie sollten ungefähr folgende Abbildung3-17 erhalten (Darstellung der Wave mit Line Between Points
:
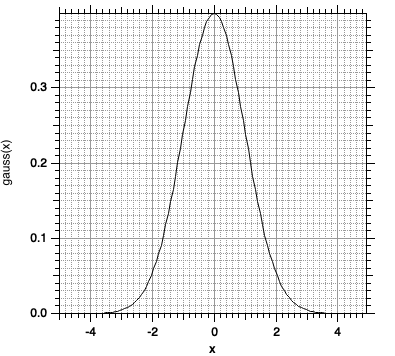
Die Gausssche Verteilungsfunktion ist in Igor eingebaut unter dem Namen gauss(x,\(\mu \), \(\sigma\)). Wir können die in Abb.3-17 dargestellt Gauss-Funktion auch wie folgt erzeugen:
Wir können die Gauss-Funktion schmaler machen (\(\sigma = 0.5\)) und ihren Schwerpunkt nach \(x=2\) versetzen (\(\mu = 2 \)):
Der Befehl appendtograph gWave2 fügt gWave2 in die existierende Abbildung ein, statt eine neue zu erzeugen (Abb. 3-18):
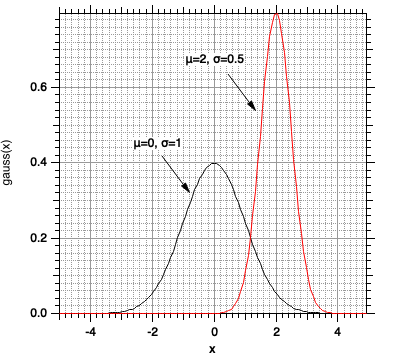
Die folgende Abb. 3-19 zeigt die Gaussfunktion für \(\mu=5,\;\sigma=1\) (Mitte) zusammen mit ihrer Stammfunktion (Integral, oben) und ihrer ersten Ableitung (unten). Wir erkennen, dass an den Punkten \(\mu \pm \sigma\) die erste Ableitung ein Maximum )\(\mu - \sigma\)) bzw. Minimum (\(\mu + \sigma\)) durchläuft.
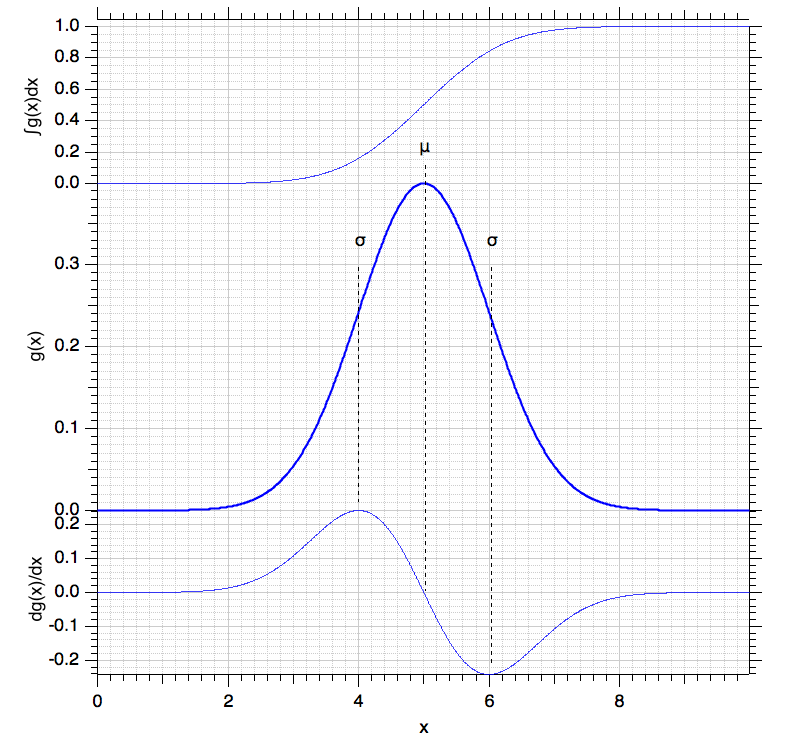
Die Halbwertsbreite (FWHM, full width at half maximum
) ist
gleich dem Abstand zwischen dem Maximum \(\mu\) der Funktion und dem Ort auf der
x-Achse, bei dem der Wert der Funktion auf die Hälfte seines Maximums
abgefallen ist. Zwischen der FWHM und der Standardabweichung \(\sigma\) besteht
die Beziehung:
\begin{equation}
{\rm FWHM} = 2 \cdot \sqrt{2 \ln 2} \cdot \sigma \approx 2,35 \cdot \sigma.
\end{equation}
Das ist aber noch nicht die gesuchte Gausssche Verteilungsfunktion. Diese hat ja mit Wahrscheinlichkeiten zu tun, und die Gesamtwahrscheinlichkeit aller Ereignisse muss gleich Eins sein. Bei den oben behandelten Histogrammen konnten wir einfach die Einzelintervalle addieren und durch die Gesamtzahl \(N\) der Ereignisse teilen; dies können wir hier nicht machen, denn die Intervalle
sind ja unendlich schmal. Aus der Summation wird hier eine Integration. Wir müssen also fordern, dass die Fläche unter der Kurve gleich Eins sein soll.
Wir lassen also ein CAS-Programm unsere Funktion \(g_{1}(x)\) von \(-\infty\) bis \(+\infty\) integrieren und finden (vgl. Abb. 3-20):
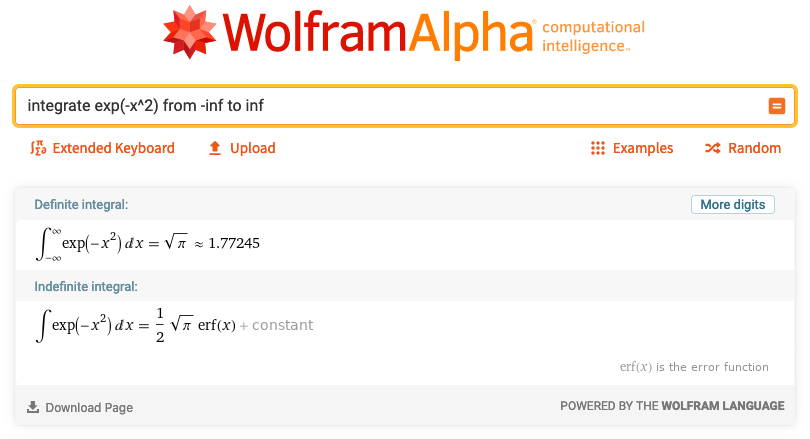
Damit können wir die Funktion so aufschreiben, dass ihr Integral Eins ergibt; wir nennen die solcherart modifizierte Funktion \(g_{2}\): \begin{equation} g_{2}(x) = \sqrt{\frac{1}{\pi}} \cdot \exp \left(- x^2\right). \end{equation}
Die Multiplikation einer Funktion mit einem Faktor, so dass ihr Integral gleich Eins wird, nennt man auch normieren. Möglicherweise ist Ihnen dies aus der Quantenchemie bekannt, wo alle Wellenfunktionen normiert sein müssen, um physikalisch sinnvoll zu sein.
... und so sieht unsere Funktion jetzt aus: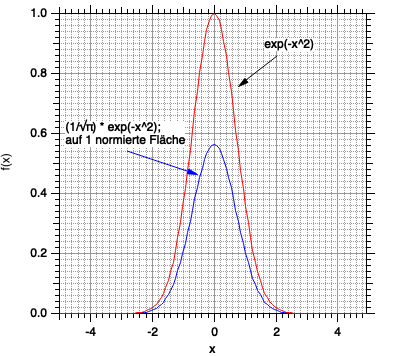
Wir sind aber noch nicht zufrieden: der Schwerpunkt der Funktion (zugleich ihr Maximum) liegt bei \(x=0\); aber wir wollen ja auch eine Verteilungsfunktion für den Fall, dass das Maximum (das wir \(\mu\) nennen wollen, es ist ja der Mittelwert) zum Beispiel bei 5 und nicht bei Null liegt. Dies erreichen wir mit einem einfachen Trick: wir subtrahieren \(\mu\) von \(x\) im Argument der Exponentialfunktion. Wir ersetzen also \(x\) in der Funktion durch \(x-\mu\). Auf diese Weise erhalten wir \begin{equation} \label{eqGaussGleichung3} g_{3}(x) = \sqrt{\frac{1}{\pi}} \cdot \exp \left(- \left(x-\mu\right)^2\right). \end{equation}
Der Trick ist ganz einfach: wenn wir den Schwerpunkt \(\mu\) von \(x\) subtrahieren, erreichen wir, dass \(x-\mu\) für \(x=\mu\) gleich Null wird, und damit der \(y\)-Wert maximal wird.
Für \(\mu = 5\) sieht unsere Funktion \(g_3\) also wie folgt aus:
\[ g_{3}(x) = \sqrt{\frac{1}{\pi}} \cdot \exp \left(- \left(x-5\right)^2\right). \]
Um eine Normierung müssen wir uns hier keine Sorgen machen: die Verschiebung des Maximums ändert am Integral unter der Gesamtkurve von \(- \infty\) bis \(+ \infty\) nichts.
Wenn wir Gl. \ref{eqGaussGleichung3} mit Gl. \ref{eqGaussFunc} vergleichen, sehen wir, dass wir schon fast fertig sind. Wir müssen aber noch eine weitere Anpassung vornehmen.
Wir haben nämlich über die Breite der Verteilung noch nichts ausgesagt.
Wir können die Funktion \(g_{3}\) breiter oder schmaler machen, wenn wir einen Faktor in den Exponenten schreiben. Schreibt man ihn als Nenner unter den Ausdruck \(\left(x-\mu\right)^2\), so wird die Glockenkurve umso breiter, je größer der Faktor wird.
Dieser Faktor hängt eng mit der bereits besprochenen Standardabweichung \(\sigma\) zusammen. Er ist nämlich ihr Quadrat. Wir schreiben nun also: \begin{equation} \label{eqGaussGleichung4} g_{4}(x) = \sqrt{\frac{1}{\pi}} \cdot \exp \left(- \frac{\left(x-\mu\right)^2}{\sigma^2}\right). \end{equation}
Leider hat diese Funktion den Haken, dass ihr Integral nicht mehr Eins ist. Durch Einsetzen der Funktion in Wolfram Alpha und Integrieren können Sie feststellen, dass das Integral der Funktion gerade gleich \(\sigma\) ist. Also müssen wir wiederum normieren: \begin{equation} \label{eqGaussGleichung5} g_{5}(x) = \frac{1}{\sigma} \cdot\sqrt{\frac{1}{\pi}} \cdot \exp \left(- \frac{\left(x-\mu\right)^2}{\sigma^2}\right). \end{equation} Wir sind praktisch fertig. Der Rest ist nur noch Ästhetik. Es ist üblich, statt des Faktors \(\pi\) den Faktor \(2\pi\) in den Nenner der Wurzel vor den Exponentialterm zu schreiben. Damit die Funktion normiert bleibt, muss dann der Term \(\tfrac{1}{2}\) in den Exponenten geschrieben werden. Damit gelangen wir zur endgültigen Funktion \(g_{6}\): \begin{equation} \label{eqGaussGleichung6} g_{6}(x) = \frac{1}{\sigma} \cdot\sqrt{\frac{1}{2 \pi}} \cdot \exp \left(- \frac{\frac{1}{2} \cdot \left(x-\mu\right)^2}{\sigma^2}\right). \end{equation}
Gl. \ref{eqGaussGleichung6} ist aber identisch mit Gl. \ref{eqGaussFunc}, das heißt wir haben die Gausssche Verteilungsfunktion anschaulich eingeführt.—
Gauss-Funktionen und Berechnung von Wahrscheinlichkeiten.–
Die Gaussche Glockenkurve \(g(x)\) (Gl. \ref{eqGaussFunc}) zeigt nicht unmittelbar eine Wahrscheinlichkeit an! Der Wert von g(x) gibt nicht etwa die Wahrscheinlichkeit dafür an, ein Ereignis am Ort \(x\) anzutreffen. Denn die Intervallbreite \(\diff x\) ist ja unendlich schmal, es passt überhaupt kein Ereignis hinein. Um zu einer finiten Wahrscheinlichkeit zu gelangen, müssen wir stets ein endliches Intervall \(\Delta x\) betrachten. Zu diesem gelangen wir, indem wir einen Bereich der Funktion der Breite \(\Delta x\) herausgreifen und über diesen integrieren. Man braucht darüber nicht zu erschrecken, denn zum Integrieren können wir ja auf Software zurückgreifen.
Die Fläche unter der Gaussschen Verteilungsfunktion \(g(x)\) entsprechend Gl. \ref{eqGaussFunc} innerhalb eines \(x\)-Intervalls \(\Delta x\) gibt die Wahrscheinlich dafür an, dass innerhalb dieses Intervalls ein Ereignis eintritt.
Ist \(g(x)\) gegeben, so ist \[ g(x) \cdot \diff{x} = \diff{W} \] gleich der infinitesimal kleinen Wahrscheinlichkeit \(\diff{W}\), dass ein Ereignis in das infinitesimal kleine Intervall zwischen \(x\) und \(x + \diff{x}\) fällt. Es ist von großer Wichtigkeit, dass \(g(x)\) nicht eine Wahrscheinlichkeit darstellt, sondern erst das Produkt \(\diff{W} = g(x)\cdot \diff{x}\). Die Funktion \(g(x)\) wird auch als Wahrscheinlichkeitsdichte bezeichnet. Entsprechend ist die (finite, nicht mehr infinitesimale!) Wahrscheinlichkeit \(\Delta W\) (und nicht mehr \(\diff{W}\)), dass ein Ereignis in das finite Intervall \(\Delta x\) zwischen \(x_{0}\) und \(x_{0} + \Delta x\) fällt, gegeben zu: \begin{equation} \Delta W = \int_{x_0}^{x_0 + \Delta x} g(x) \cdot dx. \end{equation} Erst dieses bestimmte Integral liefert eine benennbare Wahrscheinlichkeit \(\Delta W\). Die Wahrscheinlichkeit, dass ein Ereignis überhaupt irgendwo auf der \(x\)-Achse auftritt, muss gleich Eins sein, d.h. die Funktion \(g(x)\) ist so normiert, dass \[ \int_{- \infty}^{+ \infty} g(x) \cdot \diff{x} = \int_{- \infty}^{+ \infty} \diff{W} = W = 1. \] Leider ist das Integral der Gauss-Funktion nicht in geschlossener Form angebbar (wir können also nicht eine Stammfunktion in geschlossener Form hinschreiben). Die Stammfunktion hat einen Namen:Gausssche Fehlerfunktionoder
error functionoder kurz erf. Damit ist aber nichts gewonnen, weil wir keine
Formelangeben könnten, die die Gestalt dieser Funktion angeben würde. Wir müssen entweder auf tabellierte Werte zurückgreifen (das hat man in der Vergangenheit getan, es gab Riesentabellen mit Werten von erf) oder wir können ein Computerprogramm nutzen. Die gesamte Fläche unter der Glockenkurve (Gl. \ref{eqGaussFunc}) ist gleich Eins, denn die Wahrscheinlichkeit dafür, dass ein Ereignis irgendwo liegt, muss gleich Eins sein: \begin{equation} \int_{- \infty}^{\infty} g(x) \cdot dx = 1. \end{equation}
Nehmen wir an, das Maximum der Glockenkurve liege bei \(\mu=5\) und die Standardabweichung sei \(\sigma=1\). Dann lautet die Gaussfunktion für diesen Fall (da wir \(\sigma\) gleich Eins gesetzt haben, können wir diesen Faktor weglassen):
\begin{equation} \label{eqGaussFunc1} g(x) = \sqrt{\frac{1}{2 \pi}} \cdot \exp\left( - \frac{1}{2} {\left(x - 5 \right)^{2} } \right) \end{equation}Wir fragen nach der Wahrscheinlichkeit dafür, dass ein Ereignis in einem Bereich um \(\mu\) herum mit der Breite \(\pm \sigma\) liegt. Der Bereich umfasst dann das Intervall von \(4\) bis \(6\) (da ja \(\sigma = 1\)).
Die Wahrscheinlichkeit \(\Delta W\) beträgt: \begin{equation} \label{eqGaussFunc2} \Delta W = \int_{x_{0}=4}^{x_{1}=6} \sqrt{ \frac{1}{2 \pi}} \cdot \exp\left( - \frac{1}{2} {\left(x - 5 \right)^{2} } \right) \diff x. \end{equation}Wir rechnen dies mit Hilfe von Igor aus. Der Igor-Befehl zum Berechnen der Fläche unter einer Kurve lautet area(wavename, untergrenze, obergrenze). Wir erzeugen das Gaussprofil mit dem Befehl gauss(x, \(\mu\), \(\sigma\)) und berechnen die Fläche:
Wir finden als Ergebnis: \(\Delta W \approx 0,683\). Das bedeutet: mit einer Wahrscheinlichkeit von 68,3% liegt ein Wert im Intervall zwischen \(\mu - \sigma\) und \(\mu + \sigma\) (vgl. Abb. 3-19).
Im Intervall \(2 \sigma\) um das Verteilungsmaximum \(\mu\) liegen ca. \(\frac{2}{3}\) der Datenpunkte.
Im Bereich \(\mu - 2 \sigma\) und \(\mu + 2 \sigma\) liegen bereits 95.4% aller Datenpunkte:
5.5— Sogenannte Ausreißer; das Chauvenet-Kriterium.
Die Nutzung der Gauss-Funktion gestattet es, ein rationales Kriterium dafür zu finden, ob ein Punkt einAusreißerist.
Wir betrachten die folgenden Messergebnisse (dieses wurde schon eingangs dieser Vorlesung genannt und in der Abb. 4–1 dargestellt, zur allgemeinen Hebung der Motivation 😁):
{3.81599, 3.4633, 3.2439, 4.23815, 4.28283, 3.70816, 3.81192, 4.0863, 9.0238, 3.14665, 4.94752, 5.09755, 4.3839, 4.62207, 4.0626, 4.5942}
Ist der rot eingetragene Wert 9.0238 als Ausreißer zu betrachten oder nicht? Unser Kriterium soll lauten:
Ein Wert ist als Ausreißer zu betrachten, wenn die Anzahl zu erwartender Datenpunkte mit dieser Abweichung kleiner als \(\tfrac{1}{2}\) ist.
Wir gehen wie folgt vor:V_avg = 4.40805; V_sdev = 1.35289,
also \(\mu \approx 4,4\) und \(\sigma_{P}= 1,4 \).
In Igor (der fragliche Wert ist der neunte in tw, also tw[8]):
Dies ergibt: \(z = 3.41177 \approx 3.4\). Der fragliche Wert \(x_{\rm v}\) liegt 3.4 Standardabweichungen vom Mittelwert aller Messwerte entfernt.
Igor:
Als Ergebnis erhalten wir: \(\Delta W = 0.000883269\) oder 0.0883269%.
Das ist die Wahrscheinlichkeit, außerhalb des Intervalls \(\mu \pm z \cdot \sigma\) einen Punkt anzutreffen.
Unsere Liste (Inhalt von tw enthält 16 Punkte. Die Zahl an Punkten, die wir außerhalb des Intervalls \(\mu \pm z \cdot \sigma\) erwarten, ist gleich der Wahrscheinlichkeit für das Auftreten eines Punktes, multipliziert mit der Zahl der Punkte: \[ N = 16 W = 16 \cdot 0.000883269 = 0.0141323. \]
\(\mu = 4.1\) (statt wie bisher 4.4),
\(\sigma = 0.6\) statt wie bisher 1.4.
Wir sehen, dass sich der Mittelwert ändert und die Standardabweichung nur noch etwa halb so groß ist. Die Werte streuen jetzt wesentlich weniger stark.
Man darf also keineswegs einfach sagen: Der Wert liegt so und so viele Standardabweichungen vom Mittelwert weg, und muss daher ein Ausreißer sein!
Das wäre falsch. Es kommt nicht nur auf die Abweichung vom Mittelwert an, sondern außerdem auch auf die Zahl der Punkte. Bei einer Million Messpunkten würden wir in unserem Beispiel sagenhafte 16500 Punkte außerhalb von \(\mu \pm z \cdot \sigma\) erwarten!
Wir stellen das ganze Verfahren anhand eines anderen Datensatzes und die Vorgehensweise in Igor zusammen:
Solche Auswertungen haben früher (vor der Nutzung von Computern) viele Stunden gedauert; mit etwas Routine macht man das jetzt in zwei Minuten.