optische Spektroskopieeine Einschränkung dar: wir beschäftigen uns mit der spektroskopischen Untersuchung optischer Strahlung, d.h. solcher elektromagnetischer Strahlung, deren Ausbreitungscharakteristik ähnlich ist wie die von sichtbarem Licht; die mit Hilfe von Linsen und Spiegel fokussiert und reflektiert werden kann; sehr langwellige Strahlung (Mikrowellenstrahlung) und sehr kurzwellige Strahlung (harte Röntgenstrahlung) schließen wir aus.
Einige im Zusammenhang mit Strahlung wichtige Größen und ihre Einheiten
Elektromagnetische Strahlung ist zunächst durch ihre Wellenlänge \(\lambda\) charakterisiert; das ist der räumliche Abstand zwischen zwei Amplituden der Strahlung (näheres bitte in beliebigen Lehrbüchern der Physik nachschlagen; mit der Natur der elektromagnetischen Strahlung befassen wir uns hier nicht; wenn Sie von Wellen Null Ahnung haben und sich richtig tiefgehend aufschlauen wollen, empfehle ich Ihnen das Büchlein Almost All About Waves von J. R. Pierce, das man für wenig Geld bei einem bekannten Online-Buchhandel bekommt; ein richtiges Arbeitsbuch, das man mit Papier und Bleistift liest, und nach dessen Durcharbeiten Ihnen so schnell keiner mehr ein X für ein U vormachen wird.). Zwischen der Wellenlänge \(\lambda\) der Strahlung und ihrer Frequenz \(\nu\) (die Zahl von Amplituden, die je Zeiteinheit durch eine gedachte Fläche transportiert wandern) besteht die einfache Beziehung: \begin{equation} \lambda \cdot \nu = c. \end{equation} Die SI-Einheit der Wellenlänge ist das m, aber es werden im Bereich der optischen Spektroskopie fast immer die inkohärenten Einheiten \(\mu{\rm m}\), \({\rm nm}\) und Å verwendet (\(1 Å = 10^{-10}\;{\rm m} \)). Hierin ist \(c\) die Ausbreitungsgeschwindigkeit der Strahlung. Wir machen keinen großen Fehler, wenn wir annehmen, dass \(c\) in Materie denselben Wert hat wie im Vakuum: \begin{equation*} c = 299.792.458\;\frac{\rm m}{\rm s}. \end{equation*} Die Energie \(E\) eines einzelnen Lichtquants (Photonenenergie) ist gegeben zu \begin{equation} E = h \cdot \nu. \end{equation} Substituieren wir Gl. (1) in Gl. (2), so erhalten wir \begin{equation} E = \frac{hc}{\lambda}. \end{equation} Für den hier auftretenden Kehrwert der Wellenlänge gibt es eine besondere Bezeichnung: es ist die Wellenzahl \(\tilde{\nu}\), so dass \begin{equation} \label{eqErgWellenzahl} E = hc \tilde{\nu}. \end{equation}Die Wellenzahl hat die SI-Einheit \({\rm m^{-1}}\), es wird aber fast immer die inkohärente Einheit \({\rm cm^{-1}}\) verwendet.
In der konventionellen Spektroskopie ist die Wellenlänge \(\lambda\) die Messgröße; diese wird bei der Datenauswertung meistens in die Wellenzahl \(\tilde{\nu}\) umgerechnet.
Im Gegensatz zur Wellenlänge ist also die Wellenzahl der Photonenenergie proportional. Die berühmten Formeln der Atomspektroskopie (z.B. die bekannte Rydberg-Formel) verwenden die Wellenzahl statt der Wellenlänge, um den Ausdruck so einfach wie möglich zu halten.
Man könnte fragen, warum man statt der Wellenzahl nicht lieber gleich die Energie aufschreibt. Antwort: die eigentliche Messgröße in der optischen Spektroskopie ist die Wellenlänge; der Kehrwert dieser Größe ist gerade so genau wie die Messgröße selber. Dagegen war in der Vergangenheit der Zahlenwert insbesondere von \(h\) und damit die Umrechnung in eine Energie entsprechend Gl. \ref{eqErgWellenzahl} mit erheblicher Unsicherheit verbunden.
Spektroskopie ist die experimentelle Technik, einen Abschnitt des elektromagnetischen Spektrums in seine Komponenten zu zerlegen. Es ist also im Wortsinn eine Analyse-Technik.
Beispiel: Sie kennen sicher die bläuliche Flamme eines Bunsenbrenners bei genügend Luftzufuhr? Dieses bläuliche Licht wird in einem Praktikumsversuch im Rahmen des Fortgeschrittenen-Praktikums spektral zerlegt. Der experimentelle Aufbau ist in der Abb. 9-1 gezeigt:

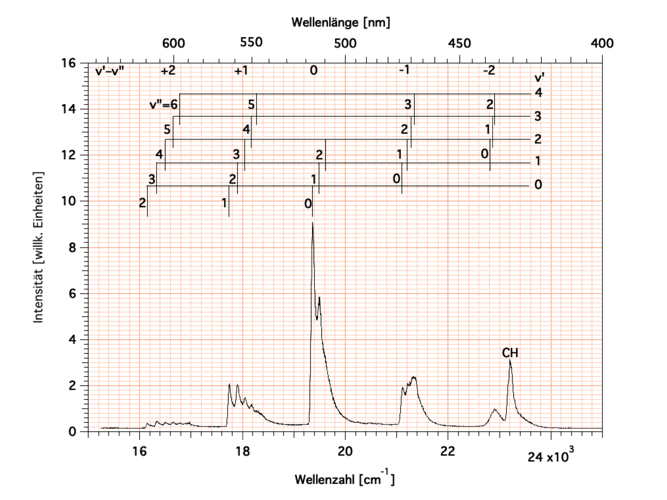
Es gibt in dieser Abbildung 2 Abszissen (x-Achsen): oben ist die Wellenlänge gezeigt, unten die Wellenzahl. Da diese Größen die Kehrwerte voneinander sind, können gleiche Intervalle nur auf einer der beiden Skalen äquidistant sein. Dies ist hier für die Wellenzahl der Fall.
Das uns weißlich-blau erscheinende Licht ist demnach aus vielen Anteilen zusammengesetzt. Mancher mag denken, unser Auge sei eine Art Spektrometer, das Wellenlängen in Farben übersetzt. Tatsächlich ist aber unser Auge als Spektrometer vollkommen ungeeignet. Anhand einer Farbwahrnehmung lässt sich keinesfalls auf eine der Farbe zugrunde liegende Wellenlänge schließen. Gelangt beispielsweise monochromatisches Licht, das für sich genommen rot erscheint (z.B. 633 nm), und monochromatisches Licht, das für sich genommen grün erscheint (z.B. 512 nm), auf dieselbe Stelle der Netzhaut des Auges, so sehen wir eine gelbe Farbe, die vollkommen unermischt erscheint; denselben Farbeindruck habe wir, wenn diese Stelle der Netzhaut mit monochromatischem Licht der Wellenlänge \(\lambda = 589\;{\rm nm}\) angeleuchtet wird. Es ist richtig, zu sagen, Licht der Wellenlänge \(\lambda = 589\;{\rm nm}\) erscheine uns gelb; aber es ist falsch, aus einem gelben Farbeindruck auf Licht der Wellenlänge \(\lambda = 589\;{\rm nm}\) zu schließen.
Womit wir es im folgenden nicht zu tun haben, ist die physikalisch-chemische Interpretation solcher Messdaten wie in der Abb. 9-2: das gehört in die Spektroskopie-Vorlesungen. Wir interessieren uns hier nur dafür, wie eine solche spektrale Auftrennung technisch bewerkstelligt wird.
Das zentrale Element eines spektroskopischen Messaufbaus ist ein Monochromator. Das ist die blaue Kiste rechts oben in der Abb. 9-1. Wir weden später einen Blick hineinwerfen. Hier nur soviel: ein Monochromator ist ein Instrument, das am Eingang einfallendes Licht ausgangsseitig in seine Komponenten zerlegt (wenn man richtig damit umgeht).
Der Aufbau eines Monochromators kann von verschiedener Art sein. Es gibt aber in jedem Monochromator ein dispergierendes Element, das ist die Vorrichtung, die die eigentliche Auftrennung bewerkstelligt.
Es gibt in der klassischen Spektroskopie zwei verschiedene dispergierende Elemente: Prismen und Gitter. Da Prismen-Monochromatoren mittlerweile eine aussterbende Spezies sind (Schreiber dieser Zeilen hat noch keinen tatsächlich in der Forschung genutzten Prismen-Monochromator gesehen), werden wir uns ausschließlich mit dem Gittermonochromator beschäftigen. Das Gitter ist also das zentrale Element eines typischen Monochromators; der Rest ist optische Peripherie, der dafür sorgen soll, dass gewisse optische Abbildungsbedingungen eingehalten werden, die wir später diskutieren werden. Zunächst interessieren uns die Eigenschaften des Gitters selber.
Ein in der Spektroskopie genutztes Gitter wird auch als Spektralgitter, Dispersionsgitter, Beugungsgitter oder Liniengitter bezeichnet.
Alles kommt darauf an, dass Sie die Eigenschaften eines Gitters verstehen lernen; der Rest ist einfach nur Abbildungsoptik, wenig verschieden von dem, was in einem Fotoapparat steckt.
Das Dispersionsgitter
Ein Dispersionsgitter ist eine transparente oder spiegelnde, ebene oder auch
gekrümmte Fläche, auf der sich in regelmäßigen Abständen parallele Ritzen oder Furchen
(Linien
) befinden. Die gesamte Fläche des Gitters ist ungefähr so groß wie ein Taschenrechner. Im Folgenden werden zunächst ebene Gitter
besprochen, bei denen die aktive Gitterfläche in einer Ebene liegt.
Typisch für ein Gitter ist die im Sonnenlicht schillernde Oberfläche, die Sie evtl. auch von CDs kennen, siehe Abb. 9-3 (CDs sind nämlich auch Gitter):

Eine graphische Darstellung eines kleinen Ausschnittes aus einem ebenen Gitter ist in der Abbildung 5 dargestellt.

Die Zahl der Linien auf einem Gitter ist ungeheuerlich groß, z.B. 1200/mm. Sie müssen vollkommen gleichförmig und in gleichen Abständen angeordnet sein (parallel). Das bedeutet, dass der Abstand zwischen zwei Linien kleiner als \(1\;\mu{\rm m}\) ist!
Die bei weitem wichtigste Charakterisierung des Gitters erfolgt durch die Angabe der Linienzahl, und zwar entweder durch
- den Abstand der Gitterlinien \(d\) oder
- die Gitterkonstante \(G\) (Zahl der Linien pro Strecke).
Schreiber dieser Zeilen hat für längere Zeit mit einem 3600-Linien-Gitter gearbeitet, für das also gilt: \(G=3600/{\rm mm}\); der Linienabstand \(d\) beträgt dann 277,8 nm.
Wir werden hier normalerweise die Gitterkonstante \(G\) verwenden, nicht den Linienabstand \(d\). Selbstverständlich lassen sich die nachfolgenden Gleichungen statt mit der Gitterkonstante auch mit dem Linienabstand notieren, da diese beiden Größen einfach Kehrwerte voneinander sind.
Wenn Sie ein Gitter kaufen, dann kaufen Sie also z.B. ein 600-Linien-Gitter; das bedeutet, dass die Gitterkonstante gleich \(G = 600 \frac{\rm Linien}{\rm mm}\) ist. Beachten Sie bitte, dass der Zähler dimensionslos ist, die Dimension der Gitterkonstante ist \({\sf L^{-1} }\), eine reziproke Länge. Die SI-Einheit ist \({\rm m^{-1}} \), aber man verwendet praktisch immer \({\rm mm^{-1}} \). Wenn Sie aber mit der Gitterkonstanten eine Rechnung ausführen, ist es klug, mit der Einheit \({\rm m^{-1}}\) zu rechnen; Sie brauchen lediglich die angegebene Gitterkonstante mit \(\tfrac{1000\;{\rm mm}}{\rm m}\) zu erweitern (multiplizieren).
Da sich der Gitterkörper mit steigender Temperatur ausdehnt, ist die Gitterkonstante temperaturabhängig. Thermisch belastete Gitter werden daher zum Teil aufwändig gekühlt.
Gitter werden sehr häufig als Reflexionsgitter betrieben, um die Absorption kurzwelliger Strahlung im Gitterkörper zu verhindern. Typische Oberflächenmaterialien sind Gold, Platin, Aluminium. Aber auch an der reflektierenden Oberfläche können Absorptionsprozesse stattfinden, insbesondere bei kurzwelligem Licht. Je streifender das Licht auf das Gitter auffällt, desto geringer ist die Absorption der Strahlung durch die Oberfläche des Gitters. Im Bereich des sichtbaren Lichtes ist die Absorption normalerweise belanglos.
Im Folgenden haben wir es viel mit Geometrie zu tun, daher zeigt die folgende Abb. 9-5 die wichtigsten geometrischen Vereinbarungen:
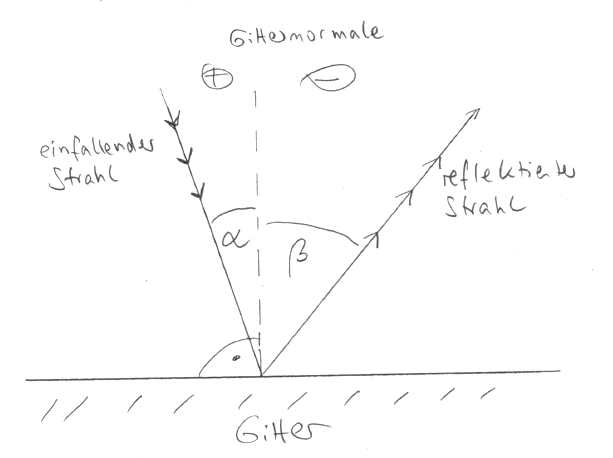
Das Gitter wird flach auf den Tisch gelegt, mit der aktiven (beleuchteten) Seite nach oben. Die durchgezogene horizontale Linie ist die aktive Fläche, von der Seite betrachtet. Darunter (schraffiert dargestellt) befindet sich der Gitterträger. Die auf die Gitterfläche senkrecht stehende, gestrichelte Linie wird Gitternormale genannt. Alle Winkel werden auf die Gitternormale bezogen, und nicht auf die Gitterfläche (sehr sehr wichtig!). Winkel nach links von der Gitternormalen sind positiv, Winkel nach rechts sind negativ (siehe eingetragenes Vorzeichen). Diese Vorzeichenkonvention ist allgemein üblich. Sie entspricht auch der alltäglichen Konvention, denn eine Drehung gegen den Uhrzeigersinn (also nach links in Abb. 9-5) entspricht einem positiven Winkel.
In der Abb. 9-5 fällt ein Lichtstrahl unter dem Winkel \(\alpha\) auf das Gitter. Wir nennen \(\alpha\) den Eintrittswinkel oder auch Einfallswinkel und betonen nochmals, dass es sich um den Winkel zwischen dem einfallenden Lichtstrahl und der Gitternormalen handelt.
\(\alpha\) ist in der Abb. 9-5 positiv und beträgt im Beispiel der Abb. 9-5 etwa \(+ 20^{\circ}\). Nach der Reflexion an der Gitterfläche verlässt der Strahl das Gitter wieder unter dem Winkel \(\beta\). \(\beta\) ist im Beispiel der Zeichnung in Abb. 9-5 negativ. Wir bezeichnen \(\beta\) als den Austrittswinkel des Lichtstrahls.
Würde es sich bei dem Gitter um einen gewöhnlichen Spiegel handeln, dann wäre \(\beta = -\alpha\) (Reflexionsgesetz), also gleich –\(20^{\circ}\). Es ist aber kein gewöhnlicher Spiegel. Um das Verhalten des Gitters zu beschreiben, müssen wir dem Lichtstrahl eine Eigenschaft zuordnen, die an sich in der Strahlenoptik nichts verloren hat: die Wellenlänge \(\lambda\) des Lichtes.
Monochromatisches Licht (Licht einer Wellenlänge \(\lambda\)), das unter dem Eintrittswinkel \(\alpha\) auf die Gitternormale fällt, wird unter einem Austrittswinkel \(\beta\) zur Gitternormalen reflektiert. Dabei wird nicht wie bei einem Spiegel das Reflexionsgesetz befolgt, sondern die Ablenkung ist wellenlängenabhängig. Verschiedenfarbiges Licht wird unter verschiedenen Winkeln reflektiert.
Die Gittergleichung
Das Verhalten eines Spektralgitters kann durch eine universelle Gleichung beschrieben werden.
Die Grundgleichung des Gitters lautet unter Verwendung der Gitterkonstanten \(G \):
\begin{equation} \label {Gittergleichung1} \boxed{\sin \alpha + \sin \beta = k \cdot G \cdot \lambda} \end{equation}Dieses ist die mit Abstand wichtigste Gleichung der spektroskopischen Messtechnik; sie wird im Folgenden erklärt. Sie ist der Ausgangspunkt aller weiteren Überlegungen. Ihre Herleitung ist sehr schwierig und setzt tiefere Kenntnisse von Beugungsphänomenen voraus. Für uns ist dies nicht notwendig. Für ebene Gitter (Plangitter) gilt G. \ref{Gittergleichung1} unmittelbar, für gekrümmte Gitter gilt sie für die Tangentialfläche an einen Gitterpunkt (geht über diese VL hinaus).
\(\alpha\), \(\beta\), \(G\) und \(\lambda\) kennen wir schon. Aber was ist \(k\)? Antwort: \(k\) ist eine kleine, ganze Zahl. Man bezeichnet sie als Gitterordnung. Eigentlich steht \(k\) sogar für eine Menge kleiner, ganzer Zahlen, z.B. (-3, -2 -1, 0, 1, 2, 3). Wie groß diese Menge ist, werden wir später erfahren, sie hängt von \(\lambda\) und \(G\) ab. Für den Moment nehmen Sie es bitte einfach hin, dass besagtes \(k\) ein Element aus einer Menge kleiner, ganzer Zahlen ist, und lassen Sie sich auf eine spätere Stelle in der Darstellung vertrösten.
Da es für \(k\) mehrere mögliche Werte gibt, ist der in Abb. 9-5 eingezeichnete unter dem Winkel \(\beta\) austretende Lichtstrahl also nicht der einzige, der das Gitter wieder verlässt. Das eingezeichnete \(\beta\) entspricht einem bestimmten \(k\)-Wert. Für andere \(k\)-Werte gibt es ebenfalls eine Reflexion, aber in eine andere Richtung (anderes \(\beta\)). Der Wert von \(\beta\) kann also nur ermittelt werden für ein bestimmtes vorgegebenes \(k\). Damit müssen wir uns jetzt beschäftigen.
Besonders interessant ist der Fall \(k=0\); dann lautet Gl. \ref{Gittergleichung1} nämlich: \begin{equation*} \sin \alpha + \sin \beta = 0, \end{equation*} und daher \begin{equation*} \sin \alpha = - \sin \beta, \end{equation*} und daher \begin{equation*} \alpha = - \beta. \end{equation*} Es ist das bekannte Reflexionsgesetz! Für \(k=0\), also in der Nullten Gitterordnung, benimmt sich ein Gitter wie ein gewöhnlicher Spiegel. Die Reflexion ist unabhängig von der Wellenlänge. Nur für \(k \neq 0\) spielt die Wellenlänge eine Rolle.
Licht, das in der Nullten Gitterordnung reflektiert wird, ist also für die Spektroskopie verloren, weil es spektral nicht getrennt wird. Die Gitterhersteller bemühen sich durch bestimmte Tricks, den Anteil des reflektierten Lichtes, der in die Nullte Gitterordnung fällt, möglichst klein zu halten.
Wenn \(\alpha\), \(\lambda\), \(k\) und \(G\) gegeben sind, kann man den Winkel des auslaufenden Strahles aus Gl. \ref{Gittergleichung1} ausrechnen:
\begin{equation} \beta = \arcsin(kG\lambda - \sin\alpha). \end{equation}
\(\arcsin\) bezeichnet die Umkehrfunktion des Sinus. Auf dem Taschenrechner ist diese Funktion häufig mit \({\sf ASIN}\) oder mit \({\sf SIN^{-1}}\) gekennzeichnet.
Besonders einfache Verhältnisse ergeben sich für senkrechten Einfall \(\alpha=0\), bei dem das Licht parallel zur Gitternormalen einfällt. (siehe Abb. 9-6): \begin{equation} k \cdot G \cdot \lambda = \sin \beta \end{equation} und damit \begin{equation} \beta = \arcsin(kG\lambda). \end{equation}
Beispiel:
Sei der Einfall parallel zur Gitternormalen (senkrechter Einfall) und die Gitterkonstante sei \(G=1200\;{\rm mm}^{-1}\).
Es falle weißes Licht im Wellenlängenbereich 400-800~nm ein. Bei welchem Winkel finden wir Licht mit \(\lambda=600\) nm in der ersten positiven Gitterordnung?
Antwort:
\begin{align*} \alpha &= 0 \\ \beta &= \arcsin\left(+1 \cdot \frac{1200}{\rm mm} \cdot \frac{\rm 10^{3}\;mm}{\rm m} \cdot 600 \cdot 10^{-9}\;{\rm m} \right) & = 46.05^0 = 0.8038 \; {\rm rad}. \end{align*}
Achtung: achten Sie bei Berechnungen unbedingt darauf, ob Ihr Taschenrechner das Ergebnis in Grad oder in rad ausgibt!
Wir betrachten jetzt Abb. 9-6.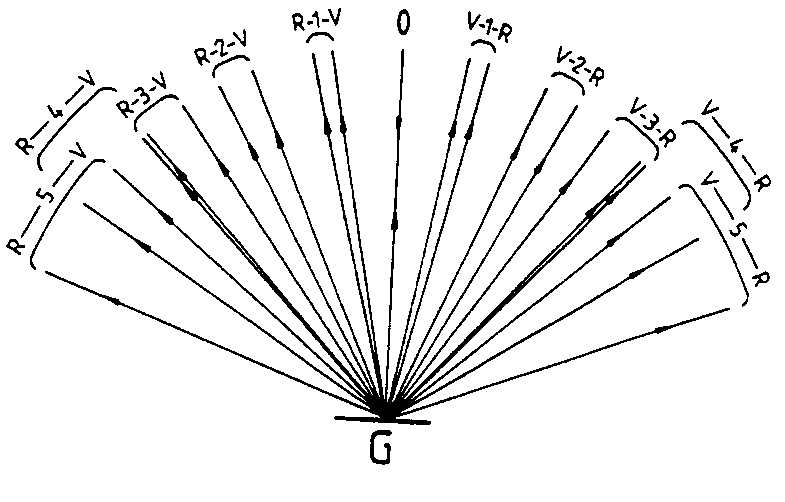
Das Licht fällt unter \(0^{\circ}\) auf das Gitter ein (\(\alpha = 0\)). Also wird das Licht in der stets unvermeidbaren Nullten Gitterordnung parallel zur Gitternormalen wieder zurückreflektiert, dieser Anteil des Strahles wird also in sich selbst zurückreflektiert und verlässt das Gitter in derselben Richtung, aus der er gekommen ist.
Rechts von der Gitternormalen, also im Bereich negativer Winkel(vgl. Abb. 9-5) sehen Sie das Symbol V-1-R über einem Winkelbereich eingetragen. V (wie violett) steht für das kürzerwellige Licht, R (wie Rot) für das längerwellige. Da das Licht in Richtung negativerer Winkel als der Gitternormalen reflektiert wird, handelt es sich um das Licht aus der ersten negativen Gitterordnung (\(k=-1\)). Der Spektralbereich von V bis R wird also in den eingezeichneten Bereich \(\Delta \beta\) winkelmäßig getrennt, oder, wie man auch sagt, Das kürzerwellige Licht ist also weniger weit von der Gitternormalen entfernt als das längerwellige. Im Grenzfall verschwindender Wellenlänge (\(\lambda \to 0\)) erfolgt die Reflexion in jeder Ordnung gerade so wie in der Nullten Ordnung; das ist auch richtig so, denn die Wellenlänge 0 ist gerade der strahlenoptische Grenzfall. In der Strahlenoptik hat das Licht keine Wellenlänge. In der Abb. 9-6 sehen Sie rechts neben dem Bereich V-1-R einen stärker aufgefächerten Bereich V-2-R; er entspricht der Reflexion des Gitters in der zweiten Gitterordnung. Würde das Licht spektral gerade eine Oktave umfassen, also zum Beispiel 400 nm bis 800 nm, dann würden die erste und die zweite Gitterordnung gerade aneinander grenzen, denn es ist natürlich für k=1 und k=2:
\begin{equation*}
1 \cdot G \cdot 800\;{\rm nm} = 2 \cdot G \cdot 400\;{\rm nm}.
\end{equation*}
Licht der Wellenlänge 400 nm wird in der zweiten Gitterordnung in gerade diejenige Richtung reflektiert, in die Licht von 800 nm in der ersten Gitterordnung reflektiert wird. Offenbar ist der Spektralbereich des Lichtes in der Abb. 9-6 keine volle Oktave, sondern kleiner, denn die erste und die zweite Ordnung grenzen nicht aneinander.
Sie erkennen aber in der Abb. 9-6, dass die vierte Ordnung etwas mit der dritten Ordnung überlappt, und die fünfte Ordnung sehr stark mit der vierten Ordnung. Dies ist ein schwerer Nachteil von Dispersionsgittern: Es gibt eine Uneindeutigkeit in der Zuordnung der Wellenlänge, weil man nicht von vorneherein weiß, aus welcher Ordnung das Licht, das in eine bestimmte Richtung reflektiert wird, denn nun stammt. Man verwendet daher häufig Filter, um z.B. kürzerwelliges Licht, das aus der zweiten Ordnung kommt und mit der ersten Ordnung überlappt, zu unterdrücken.
aufgelöst
.
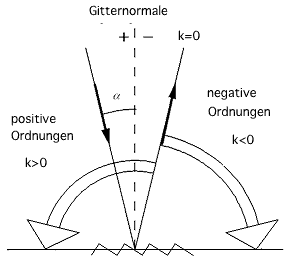
Vorzeichen der Gitterordnungen:
Man geht von der Nullten Ordnung aus (\(k=0\), s. Abb. 9-7, wo das Licht von links einfällt ( \(\alpha > 0\)) und nach rechts (\(\beta < 0\)) entsprechend dem Reflexionsgesetz wieder austritt). In positiven Gitterordnungen erscheint das reflektierte Licht links von der Reflexion in Nullter Ordnung (\(k=0\)). Es gilt:\(\beta > - \alpha\) für positive Ordnungen (\(k>0\)),
\(\beta < - \alpha\) für negative Ordnungen (\(k<0\)),
\(\beta = - \alpha\) für die Nullte Ordnung (\(k=0\)).
Dieser Zusammenhang ist in der Abb. 9-7 graphisch dargestellt.
Zahl der auftretenden Gitterordnungen:
Jetzt sind wir endlich in der Lage, den schon weiter oben angesprochenen Wertebereich von \(k\), also die Zahl tatsächlich auftretender Gitterordnungen, zu bestimmen. Diese Zahl ist endlich, da der Sinus der Winkel \(\alpha\) und \(\beta\) entsprechend Gl. \ref{Gittergleichung1} zusammen genommen nicht größer als 2 sein kann (weil der Sinus eine Zahl ist, die nicht größer als Eins und nicht kleiner als -1 sein kann, also ist die Summe eine Zahl im Intervall zwischen -2 und +2). Es muss also gelten:\begin{equation} |kG\lambda| \leq 2 \end{equation}
und, da \(\lambda\) und \(G\) beide positive Zahlen sind,\begin{equation} |k| \leq \frac{2}{G \lambda}. \end{equation}
Wenn \(G\lambda \ll 1\), können viele Ordnungen auftreten.
Es gibt für ein gegebenes Gitter und eine gegebene Wellenlänge eine größte positive und eine kleinste negative Beugungsordnung. Falls der Eintrittswinkel \(\alpha = 0\), stimmen diese beiden Beugungsordnungen betragsmäßig überein, weil die Abstrahlcharakteristik des Gitters zu beiden Seiten der Nullten Ordnung (die für diesen Fall mit der Gitternormalen zusammenfällt) symmetrisch ist (vgl. Abb. 9-6), aber für \(\alpha \neq 0\) können Sie sich \(|k_{\rm max}|\) und \(|k_{\rm min}|\) unterscheiden, weil auf der einen Seite der Nullten Ordnung mehr Platz
ist als auf der anderen (vgl. Abb. 9-7).
Der Austrittswinkel \(\beta\) kann beim Reflexionsgitter nie größer als \(90^{^0}\) werden, sonst würde das Licht nicht austreten sondern im Gitterkörper verschwinden. Da der Austrittswinkel \(\beta\) mit steigender Wellenlänge zunimmt, gibt es für jede Gitterordnung eine maximale Wellenlänge; das ist diejenige Wellenlänge, bei der das Licht das Gitter parallel zur Oberfläche (senkrecht zur Gitternormalen) verlässt.
Die Winkeldispersion - eine wichtige Hilfsgröße
In der nächsten Vorlesung werden wir lernen, wie ein Gitter in einem Monochromator funktioniert. Zur Vorbereitung dessen bringen wir zunächst die grundlegende Gittergleichung (Gl. 9–5) in eine differentielle Form.
Zur Erinnerung: die Grundgleichung des Spektralgitters lautet:
\begin{equation*} \sin \alpha + \sin \beta = k \cdot G \cdot \lambda. \end{equation*}Ändert sich bei festgehaltenem Einfallswinkel \(\alpha\) die Wellenlänge \(\lambda\) der Strahlung, so ändert sich auch der Austrittswinkel \(\beta\) (Ausnahme ist natürlich die Nullte Gitterordnung).
Wir fragen nun danach, um wieviel sich \(\beta\) ändert, wenn sich \(\lambda\) ändert, d.h. wir fragen nach \(\tfrac{\diff \beta}{\diff \lambda}\) und bezeichnen diese Größe als Winkeldispersion \(D_{\beta}\):
\begin{equation} \label{eqDefD_beta} D_{\beta} = \frac{\diff \beta}{\diff \lambda} \end{equation} \(D_{\beta}\) ermitteln wir, indem wir die Grundgleichung des Gitters nach \(\beta\) auflösen (wurde bereits in VL 10 gezeigt): \begin{equation*} \beta = \arcsin(k \cdot G \cdot \lambda - \sin \alpha). \end{equation*} Leiten wir \(\beta\) nach \(\lambda\) ab (XCAS oder ein anderes Programm für symbolische Mathematik), so finden wir: \begin{equation} \label{eqD_beta} D_{\beta} = {\frac {{k}\,{G}}{\sqrt {1- \left( {k}\,{G}\,\lambda -\sin \alpha \right) ^{2}}}}. \end{equation} Für senkrechten Einfall (\(\alpha = 0\)) vereinfacht sich die Gleichung zu \begin{equation} D_{\beta} = {\frac {{k}\,{G}}{\sqrt {1- \left( {k}\,{G}\,\lambda \right) ^{2}}}}. \end{equation} Gl. 13 können wir noch anders formulieren: \begin{align*} \sin \beta &= k \cdot G \lambda \\ \sin^2 \beta &= k^2 \cdot G^2 \lambda^2 \\ \sin^2 \beta + \cos^2 \beta &= 1 \\ \cos^2 \beta &= 1-\sin^2 \beta \\ \cos^2 \beta &= 1- k^2 \cdot G^2 \lambda^2 \\ \cos \beta &= \sqrt{ 1- k^2 \cdot G^2 \lambda^2 } \\ \end{align*} Daher kann die Winkeldispersion bei senkrechtem Einfall auch geschrieben werden als: \begin{equation} D_{\beta} = \frac {kG} { \cos \beta}. \end{equation}Beispiel: Welche Winkeldispersion weist ein Plangitter mit der Gitterkonstante \(G=1204,3/{\rm mm}\) bei einer Wellenlänge von 254,95 nm in der zweiten negativen Gitterordnung auf bei einem Eintrittswinkel des Lichtes von \(\alpha = 8,5375^{\circ}\) auf?
Antwort: die angegebenen Parameter können sofort in Gl. \ref{eqD_beta} eingesetzt werden:
\begin{equation*} D_{\beta} = {\frac {{-2}\cdot {1204,3 \cdot 10^3\; {\rm m^{-1}}}}{\sqrt {1- \left( {-2}\cdot {1204,3 \cdot 10^3\; {\rm m^{-1}}}\cdot 254,95\cdot 10^{-9}\;{\rm m} -0,14846 \right) ^{2}}}}. \end{equation*}Ausrechnen liefert das Ergebnis:
\begin{equation*} D_{\beta} = -3\;723\;009\;{\rm m^{-1}} \end{equation*} Diese Antwort ist zwar numerisch richtig, aber wir können nichts damit anfangen. Die Einheit \({\rm m^{-1}}\) bezieht sich aufgrund der Definition von \(D_{\beta}\) offenbar auf die Wellenlänge. Wir ersetzen daher die Einheit m durch nm: \begin{equation*} D_{\beta} = \frac{-3\;723\;009}{10^{9}\;\rm nm} = - 3,7230 \cdot 10^{-3}\;{\rm nm^{-1}}. \end{equation*} Es handelt sich um eine Winkeländerung als Folge einer Wellenlängenänderung. DienatürlicheEinheit des Winkels ist das \({\rm rad}\). Unser Ergebnis muss daher um die Pseudo-Einheit
radergänzt werden: \begin{equation*} D_{\beta} =- 3,7230 \cdot 10^{-3}\;\frac{\rm rad}{\rm nm}. \end{equation*} Das ist immer noch sehr unanschaulich; wir drücken den Winkel lieber in der Einheit Grad aus und bedenken, dass \(2 \pi = 360^{\circ}\): \begin{equation*} D_{\beta} =\frac {- 0,21331^{\circ}}{\rm nm}. \end{equation*}
Jetzt können wir das Ergebnis verstehen: Wenn sich die Wellenlänge von \(\lambda = 254,95\cdot 10^{-9}\;{\rm m}\) um 1 nm vergrößert, dann ändert sich der Winkel um \( - 0,21331^{\circ} \).
Das negative Vorzeichen vor dem Winkel besagt, dass der austretende Lichtstrahl weiter nach rechts gedreht wird, vgl. Abb. 9-7 dieser Vorlesung. Das muss auch so sein, denn wir haben die zweite negative Gitterordnung angenommen. Der Winkelabstand zur Nullten Ordnung wird um diesen Betrag größer, und wegen der Vorzeichenkonvention wird der Winkel um diesen Betrag negativer.
