
Messen in der Chemie
Achte Vorlesung
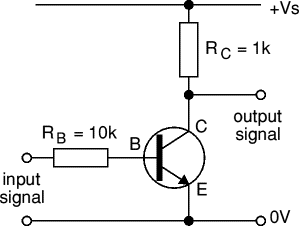
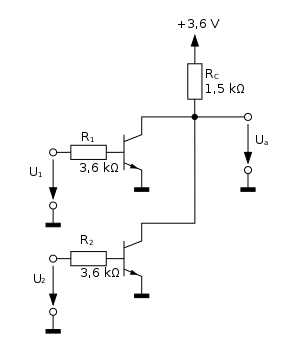
logisch NULLund
logisch EINSgenannt) zu einem ebenfalls binären Ausgangssignal verarbeitet. Es handelt sich also um eine Art der Signalverarbeitung.
| Ausgang | Eingang | |
| Eins | [(+4V) … (+12V)] | [(+3V) … (+12V)] |
| Null | [(-2V) … (+1V) ] | [(-2V) … (+1.5V) ] |
| Ausgang | Eingang | |
| Eins | [(+2.4V) … (+5V)] | [(+3V) … (+12V)] |
| Null | [(0V) … (+0.4V)] | [(0V) … (0.8V)] |

Truth tableund auf deutsch
Wahrheitstabellegenannt. Für das NOT-Gate sieht sie wie folgt aus:
| IN | OUT |
| 0 | 1 |
| 1 | 0 |
| IN1 | IN2 | OUT |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
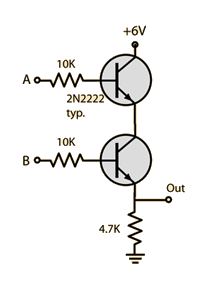
| IN1 | IN2 | OUT |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
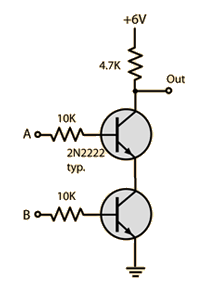
| IN1 | IN2 | OUT |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
| IN1 | IN2 | OUT |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
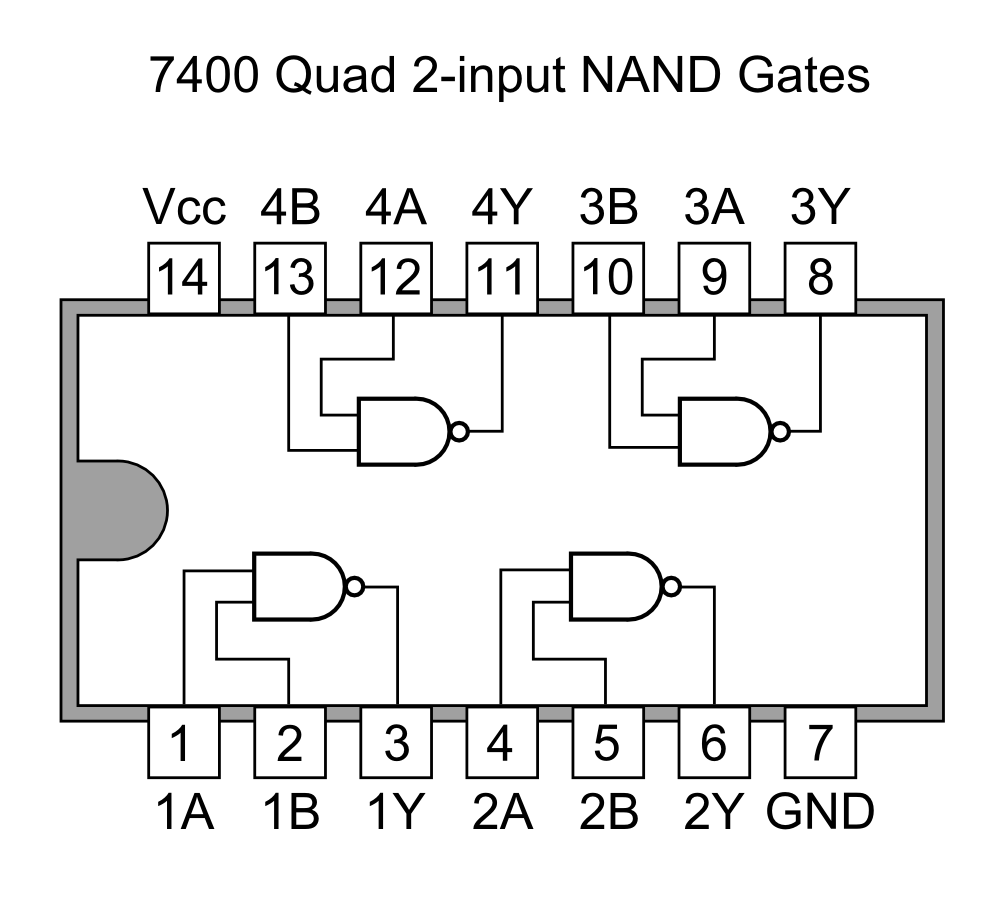
| IN1 | IN2 | OUT |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Der Schmitt-Trigger steuert beim Erreichen einer bestimmten Eingangsspannung \(V_{\rm in}\) schlagartig durch (geht von NULL nach EINS) und bleibt in diesem Zustand, bis die Eingangsspannung ein anderes, niedrigeres Niveau als \(V_{\rm in}\) unterschreitet. Er schaltet also zum Beispiel bei \(V_{\rm in} = 1{\rm\;V}\) auf EINS, und geht beim Herunterfahren der Eingangsspannung erst bei \(V_{\rm in} = 0,6{\rm\;V}\) wieder auf NULL (dies war nur ein willkürlich gewähltes Zahlenbeispiel). Man nennt dieses Verhalten Hysterese.
Wir betrachten zunächst die Schaltung, die in der Abbildung 8-4 gezeigt ist. Den Widerstand RB ignorieren wir. Die Betriebsspannung beträgt +V (z.B. 12V), und es gibt eine Eingangsspannung \(V_i\); das ist die Signalspannung, auf die der Trigger reagiert, indem er die ausgangsseitige Spannung \(V_0\) auf +1 oder auf Null setzt. \(V_0\) wird gegen Masse (Null Volt) ganz unten im Bild gemessen, also über die Spannungsabfälle an RE und an der Emitter-Kollektorstrecke von T2.
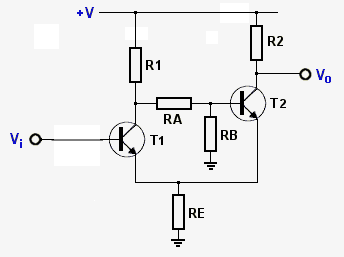
Die beiden Transistoren T1 und T2 sind auf zweierlei Weise verkoppelt:
Wir nehmen zunächst an, es liege keine Eingangsspannung \(V_i\) an der Basis von T1 an. Dann sperrt T1, es fließt kein Kollektorstrom, an \(R_{1}\) fällt keine Spannung ab (Ohmsches Gesetz, U=R*I, wenn I=0 ist auch U=0 !), und der Kollektor von T1 liegt praktisch auf dem positiven Potential der Versorgungsspannung (also hier 10V). Es gibt eine Widerstandskaskade R1-RA-R(BE)-RE, der die Basisvorspannung von T2 festlegt. Die Vorwiderstände R1 und RA vor der Basis von T2 sind so dimensioniert, dass T2 vollständig leitet (in Sättigung arbeitet
), dass also der Widerstand der Emitter-Kollektor-Strecke von T2 den minimalen überhaupt möglichen Wert angenommen hat (und daher der maximal mögliche Strom für die gegebene Versorgungsspannung fließt). Über Emitter und Kollektor von T2 fällt dann nur eine geringe Spannung ab. \(V_0\) wird weitgehend durch R2 und RE festgelegt. "Unterhalb" des Transistors T2 (am Emitter) beträgt die Spannung gegen 0V also ebenfalls \(V_0\): das Emitterpotential von T2 (die Spannung zwischen dem Emitter von T2 und 0V) beträgt \(V_0\).
Das Emitterpotential von T2 (also \(V_0\)) liegt auch am Emitter von T1 an und es ist positiv (z.B. \(V_0\)=1000mV). Damit T1 leitfähig werde, muss seine Basisvorspannung um ca. +700mV positiver sein als das Potential am Emitter (es kommt ja auf die Basis-Emitter-Spannung an), wir brauchen also in diesem Zahlenbeispiel eine Vorspannung von +1700mV, damit T1 leitfähig werde.
Wenn \(V_i\) allmählich ansteigt, geschieht zunächst nichts, bis es einen Wert von ca. +700mV positiver als das Emitterpotential von T1 ist. Erst dann zieht T1 einen Basisstrom und wird auch Emitter-Kollektor-seitig leitfähig. Der Widerstand der Emitter-Kollektor-Strecke von T1 bricht zusammen, und praktisch die gesamte Vorspannung +V fällt an R1 ab (ein kleiner Teil wird auch an RE abfallen, es soll aber gelten R1>>RE). Dadurch beginnt T2, sich abzuschalten, der Widerstand der Emitter-Kollektor-Strecke von T2 wird größer. Daher ändert sich das Spannungsteiler-Verhältnis R2 - T2 - RE, mehr Spannung fällt an T2 ab, und das Emitterpotential von T2 wird weniger positiv. Damit wird auch das Emitterpotential von T1 weniger positiv, die Basis-Emitter-Spannung von T1 steigt, und T1 wird erst recht leitfähig. Dies ist ein Beispiel einer positiven Rückkopplung. Die positive Rückkopplung fixiert den neuen Zustand, in dem T1 leitet und T2 gesperrt ist. \(V_0\) ist jetzt nahezu gleich der positiven Versorgungsspannung +V, weil T2 sperrt, durch R2 folglich kein Strom fließt und daher keine Spannung abfällt. Das Potential am Emitter von T2 ist jetzt praktisch gleich Null, da ja praktisch die gesamte Spannung an der Emitter-Kollektor-Strecke von T2 abfällt. Daher ist auch das Emitterpotential von T1 in diesem Zustand gleich Null, und nicht mehr gleich 1000mV.
Jetzt nehmen wir an, dass Vi wieder Richtung Null abfällt. Die Emitterspannung von T1 ist jetzt nicht mehr gleich +1000mV, sonder ungefähr gleich Null mV. T1 bleibt also leitend, bis die +700mV unterschritten sind. Erst dann sperrt T1 und T2 wird wieder leitend.
Resultat: T1 wird leitfähig, wenn eine Basisvorspannung von +1700mV überschritten wird, und wird erst wieder nicht-leitend, wenn eine Basisvorspannung von +700mV unterschritten wird. Der Trick ist also, dass der Zustand von T2 das Emitterpotential von T1 einstellt und damit die Baisvorspannung von T1 festlegt, ab der T1 leitend bzw. nicht-leitend wird.
Also:
Die Hysterese des Schmitt-Triggers kommt dadurch zustande, dass der Emitter von T1 in den beiden Zuständen auf unterschiedlichem Potential liegt und dadurch eine andere Basis-Vorspannung erforderlich ist, um ihn zu sperren, als ihn leitend zu machen.
Die Abb. 8-4a zeigt, wie der Schmitt-Trigger auf ein Eingangs-Signal reagiert.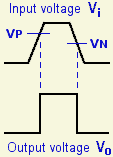
Schmitt-Trigger und ähnliche Schaltungen nennt man auch Komparatoren, weil sie ein Eingangssignal mit einer vordefinierten Schwelle vergleichen und erst ab dem Erreichen dieser Schwelle durchschalten. Der Schmitt-Trigger ist also ein Komparator mit Hysterese. Dies wird auch genutzt, um verrauschte Eingangssignale zu normalisieren, also in einen definierten Puls umzusetzen. Dies ist in der nachfolgenden Abb. 8-4b gezeigt.
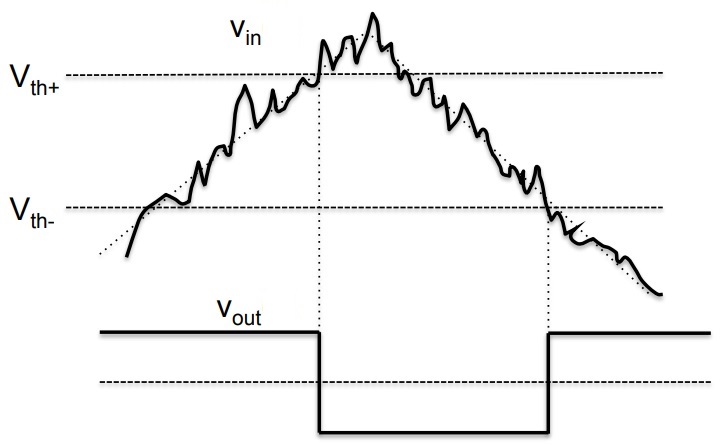
Ein Komparator ohne Hysterese wäre instabil, insbesondere wenn das Eingangssignal verrauscht ist. Wenn nämlich das verrauschte Eingangssignal den Schwellenwert erreicht, würde das Rauschen immer wieder oberhalb und unterhalb der Schwelle liegen, und daher würde das Ausgangssignal immer wieder gestartet und gestoppt.
Nehmen wir als Beispiel das Eingangssignal für eine Temperaturkontrolle, und der Ausgang des Komparators (der eine kritische Temperatur detektieren soll) sei an einen Lebensfunktionsmonitor eines Patienten angeschlossen. Das Ausgangssignal des Komparators würde erratisch ein- und ausschalten und damit keine zuverlässige Messung der Temperatur darstellen.
Die Hysterese sollte also größer sein als das Signal-Rauschen.
voll leitend(maximaler Stromfluss aus dem Kollektor) oder
voll sperrend(praktisch gar kein Kollektorstrom). Diesen beiden Zuständen der Schaltung kann man eine
logische Nulloder eine
logische Einszuordnen, und damit bilden Sie den Ausgangspunkt der Digital-Elektronik.
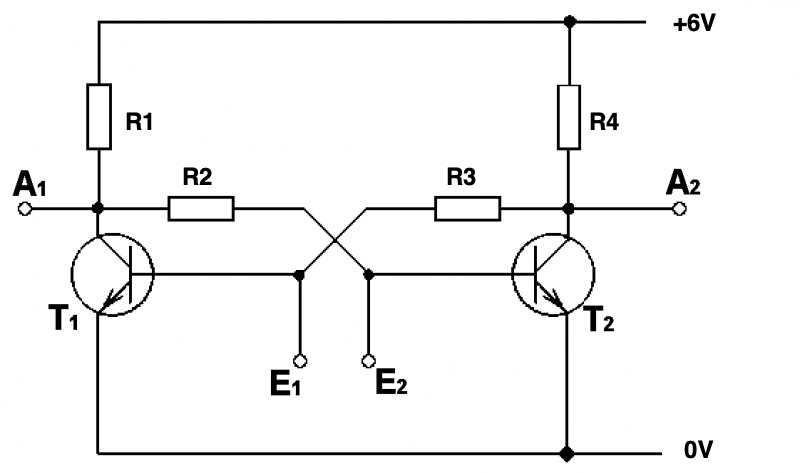
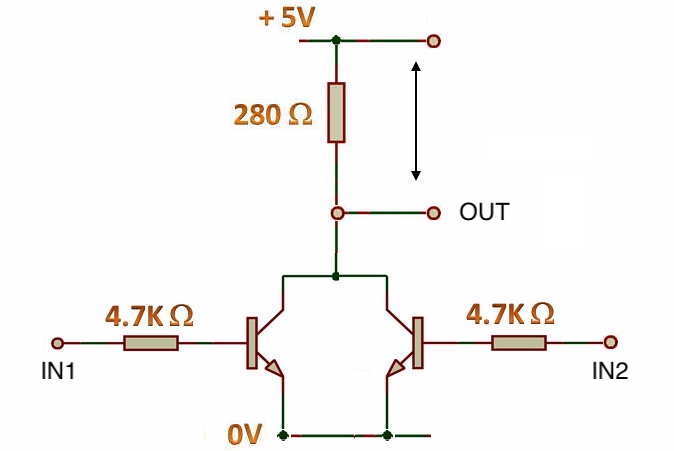
Die Frage ist nur, bei welchem Transistor dies als erstes geschieht. Die verwendeten Bauelemente sind ja nicht vollständig identisch, sondern durch Exemplarstreuungen charakterisiert. Einer der beiden Transistoren wird also eher durchsteuern als der andere.
Wir nehmen willkürlich an, dass T2 eher durchsteuert als T1. Dann liegt der Kollektor von T2 praktisch auf dem Emitterpotential von T2 (Widerstand EC sehr klein), so dass auch die linke Seite von R3 auf Emitterpotential liegt. Die Basisvorspannung von T1 fällt dadurch praktisch auf Null ab und der Transistor sperrt. Wenn T2 als erstes durchsteuert, wird T1 wegen der Kopplung seiner Basis über R3 mit dem Kollektor von T2 zwangsläufig gesperrt. Der Widerstand EC von T1 ist damit nahezu unendlich, an R1 fällt demnach praktisch keine Spannung ab, und T2 steuert erst recht durch.
Dieser Zustand bleibt für immer stabil. Wenn T2 als erster durchsteuert, bleibt er solange durchgesteuert, bis man die Stromversorgung wieder abtrennt. Wir messen das Ausgangssignal an A1 gegen Null Volt. Der Spannungsabfall an R1 ist praktisch Null, also zeigt A1 gegen Null Volt praktisch die Versorgungsspannung; diesen Zustand kann man "high" oder auch "Eins" nennen. Am Ausgang A2 ist es genau umgekehrt, wenn A1 auf "Eins" steht, zeigt A2 "Null" an (praktisch keine Potentialdifferenz zwischen A2 und 0V, da die EC-Strecke von T2 extrem niederohmig ist.
(Wenn wir A1 bzw. A2 gegen +6v statt gegen Null Volt messen würden, würde sich alles genau umkehren. Es kommt also auf das Bezugspotential an.)
Würde zufälligerweise beim Einschalten T1 als erstes leitfähig werden, so würden sich diese Verhältnisse genau umkehren. Bei der gezeigten Schaltung ist es gerade dann, wenn die Bauelemente in ihren Spezifikationen sehr ähnlich sind, unmöglich, vorherzusagen, welcher Ausgang auf "Eins" und welcher auf "Null" liegen wird.
Wir betrachten nun die zusätzlichen Eingänge E1 und E2. Wir nutzen sie, um einen negativen Puls auf T1 bzw. T2 zu setzen. Dies könnte man z.B. dadurch realisieren, dass man vom Punkt E1 bzw. E2 einen Tastschalter Richtung Null Volt legt.
Wir wollen bei der Annahme bleiben, dass T2 durchgesteuert ist, T1 folglich sperrt und der Ausgang A1, gegen Null Volt gemessen, als Konsequenz dessen auf "Eins" liegt. Betätigt man nun den Tastschalter am Eingang E2, so wird zwischen der Basis von T2 und Null V kurzeitig eine leitende Verbindung hergestellt. Da der Emitter von T2 ohnehin mit Null V verbunden ist, ist die Basis-Emitter-Kreis von T2 also kurzzeitig kurzgeschlossen. Folglich sperrt T2; also ist die EC-Strecke von T2 hochohmig, also fällt an R4 praktisch keine Spannung mehr ab, also wird die Basis von T1 "hochgelegt", T1 steuert durch, an R1 fällt praktisch die gesamte Betriebsspannung ab, und die Basis von T2 liegt mehr oder weniger auf Emitterpotential, und das auch dann, wenn wir den Schalter E2 wieder loslassen, denn was soll sich ändern? Die Basis von T2 ist ja nach dem Loslassen immer noch praktisch auf Emitterpotential. Der neue Zustand bleibt also erhalten. Jetzt liegt also A1 auf Null und A2 auf Eins.
Wie kommen wir wieder zurück zur ursprünglichen Situation? Ganz einfach indem wir kurz den Schalter E1 betätigen und damit den Basis-Emitterkreis von T1 kurzschließen. Es geschieht dann dasselbe wie eben, nur mit ausgetauschten Ziffern "1" und "2".
Der in dieser Vorlesung gezeigte Flipflop ist sozusagen das Elementarmodell, das aber schwere Nachteile hat. Hier seien nur zwei aufgeführt:
Messen in der Chemiesprengen. Die wesentlichen Merkmale der bistabilen Kippstufe konnten an dem einfachen Beispiel der Abb. 8-5 ja klar gezeigt werden.
Verschiedene Arten von Flipflops (unser Flipflop ist zum Beispiel ein primitiver RS-Flipflop) sind problemslos als integrierte Schaltkreise für wenige Cent erhältlich.
mit GewaltLadungen von der einen zur anderen Platte bewegen. Der Pluspol der äußeren Spannungsquelle saugt Elektronen von der einen Platte ab, der Minuspol gibt Elektronen an die andere Platte ab. Das Resultat besteht darin, dass die Platten sich um eine Ladungsmenge \(2 Q\) unterscheiden. Die Ladungsmenge \(Q\) wurde von der einen Platte abgezogen und auf die andere Platte transportiert.
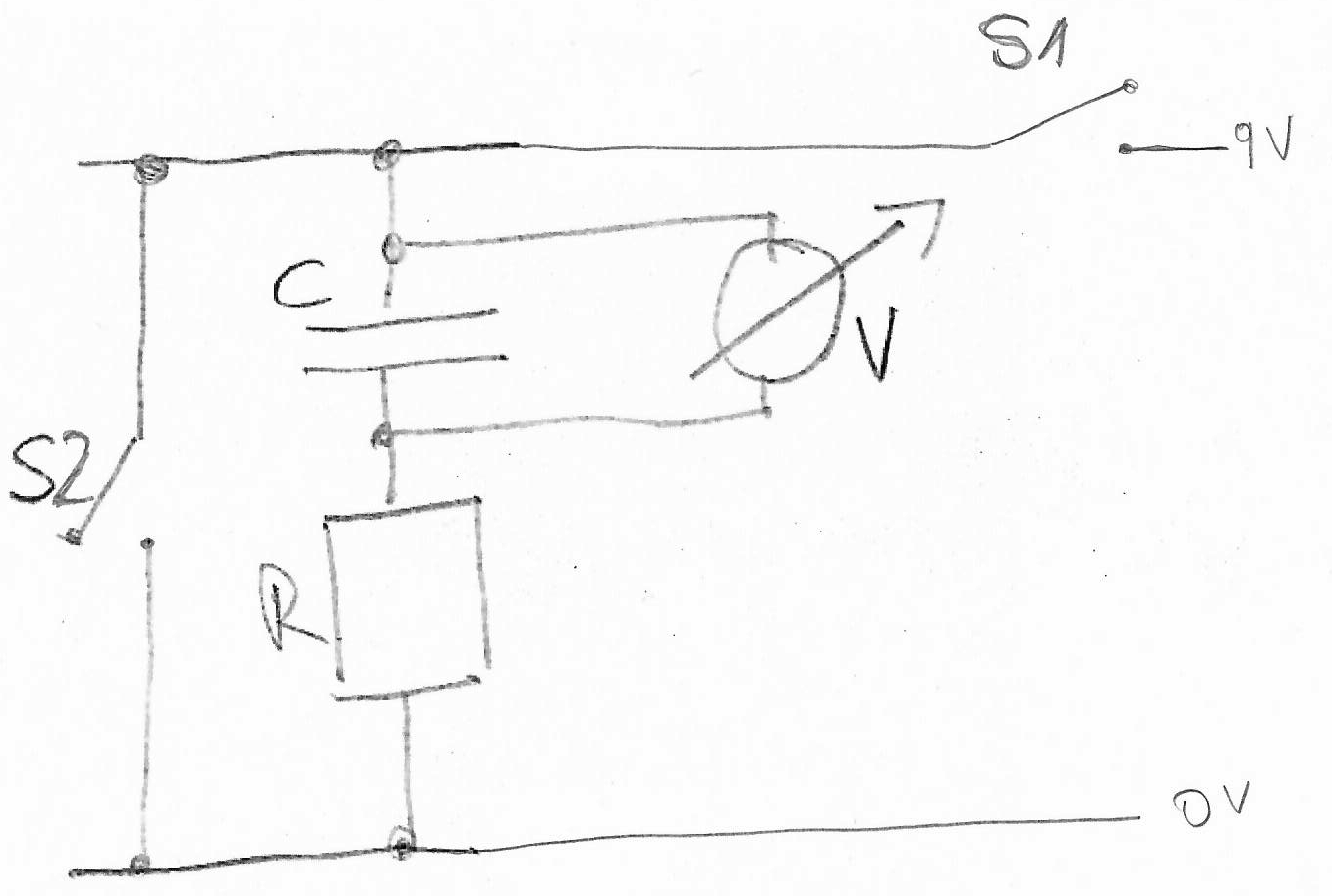
Durch Messung stellt man fest, dass \[ k = \frac{1}{RC}. \] Für die zeitliche Änderung der Spannung am Kondensator während des Entladevorganges gilt demnach die einfache Gleichung: \begin{equation} U_C(t) = U(t=0) \cdot \exp \left(-\frac{t}{R \cdot C} \right) \end{equation} Es handelt sich also um eine exponentiell mit der Zeit fallende Spannung. Beachten Sie, dass die Größe \(R \cdot C\) die Dimension einer Zeit hat (nachrechnen!). Sie wird als Zeitkonstante bezeichnet.
Lädt man den Kondensator über einen Widerstand \(R\) auf, so steigt die Spannung gemäß \begin{equation} \label{eqKondensatorSpannungAufladung} U_C(t) = U(t=0) \cdot \left( 1 - \exp \left(-\frac{t}{R \cdot C} \right)\right); \end{equation} dies ist eine sogenannte Sättigungsfunktion.
Die Serienschaltung von Kondensator und Widerstand, das RC-Glied, ist für die Elektronik von größter Bedeutung.
Mehr müssen wir im Augenblick nicht wissen.
Wenn das RC-Glied die Basis-Vorspannung eines Transistors beeinflusst, wird der Transistor irgendwann (je nach Schaltung) in den leitenden bzw. in den gesperrten Zustand übergehen. Wir haben damit eine Zeitabhängigkeit eingeführt und wollen diese zunächst an einer einfachen Schaltung betrachten.
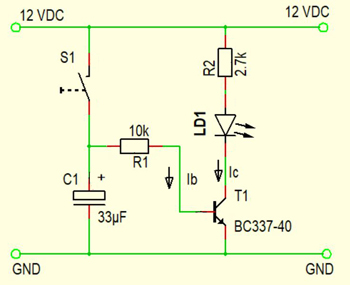
Abb. 8-7 zeigt die grundsätzliche Schaltung. Der Schalter S1 ist ein Taster, der nur solange geschlossen ist, wie man ihn gedrückt hält. Wenn der Kondensator entladen ist und S1 nicht gedrückt wird, liegt an der Basis von T1 überhaupt keine Spannung an, also sperrt der Transistor und LD1 leuchtet nicht.
Drücken wir den Taster und halten ihn gedrückt, so stellen wir damit eine leitende Verbindung zur +12V-Spannungsversorgung her. Das hat zwei Effekte:
Im ersten Augenblick ist die Spannung am positiven Pol des Kondensators (oben in Abb 9-7) gleich 12 V, denn auf diese Spannung wurde er aufgeladen. Damit kann C1 als eine Art Spannungsquelle fungieren, und von C1 ausgehend kann ein Strom durch R1 und die Basis-Emitter-Strecke fließen, gerade so wie vorher von der externen 12-V-Spannungsquelle. Durch den Stromfluss entlädt sich der Kondensator mit der Zeitkonstante \(RC=10\;{k\Omega} \cdot 33\;{\rm \mu F} = 0,33\;{\rm s}\). Nach 0,33 s ist die Spannung auf 1/e der ursprünglichen Wertes von 12V abgefallen, das sind etwa 36%, also auf 4,4 V → immer noch genug für T1; nach weiteren 0,33 s beträgt die Spannung noch ca. 1,6 V (reicht immer noch aus), nach weiteren 0,33 s (also nach insgesamt etwa 1 s) liegen noch 0,59 V an. Damit geht der Transistor in den nicht-leitenden Zustand über, folglich sperrt auch die Kollektor-Emitter-Strecke und LD1 erlischt.
Für eine genauere Betrachtung müssten wir auch den Widerstand der Basis-Emitter-Strecke berücksichtigen; diese ist aber klein gegen die \(10\;{k \Omega}\) des Vorwiderstandes R1.
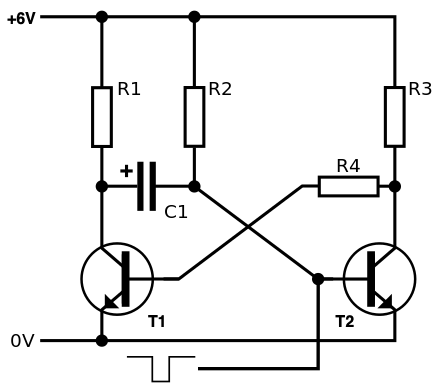
Monoflopgenannt). Bitte vergleichen Sie die Schaltskizze genau mit derjenigen der Abb. 8-5. Der entscheidende Unterschied ist, dass hier einer der beiden Widerstände durch einen Kondensator ersetzt ist.
Vor der Basis von T2 gibt es außerdem eine Verbindung zu einem Tastschalter, mit dessen Hilfe ein negativer Puls an die Basis von T2 gegeben werden kann.
Die Schaltung hat eine Normalzustand
("Aus"-Zustand, der stabile Zustand) und einen "An"-Zustand (der instabile Zustand), der sich nur einstellt, nachem der Taster gedrückt wurde.
Im Normalzustand ist T2 leitend, denn der Transistor ist über R2 mit der positiven Versorgungsspannung verbunden. Dann liegt der Kollektor von T2 praktisch auf Emitterpotential, und an der Basis von T1 liegt praktisch keine Spannung an. Der Kondensator C1 ist in diesem Zustand belanglos; da die Ausgangsseite von T1 hochohmig ist, liegt die linke Seite von C1 praktisch auf dem Potential der Versorgungsspannung; die rechte Platte liegt auf dem Potential der Basisvorspannung von T2, also etwa 700mV. Da der Kondensator geladen ist (linke Platte: +6V; rechte Platte: +0.7V; als ist \(U = 5.3\;{\rm V}\)), durchfließt ihn kein Strom.
Aber jetzt! Wenn wir der Basis von T2 einen negativen Puls verpassen, sperrt T2 augenblicklich (es ist ja ein npn-Transistor, der eine positive Vorspannung vor der Basis benötigt). Also ist die Emitter-Kollektor-Strecke sehr hochohmig, es fließt kein Strom, an R3 fällt keine Spannung ab, und die rechte Seite von R4 liegt praktisch auf dem Potential der Versorgungsspannung.
Damit wir T1 sofort leitend, denn die Schleusenspannung der Basis von T1 ist überschritten. Damit bricht der Widerstand seiner Emitter-Kollektor-Strecke zusammen, die Betriebsspannung fällt jetzt fast vollständig an R1 ab, und die linke Seite von C1 liegt auf einem Potential von wenigen hundert Millivolt. Da sich der Ladungszustand von C1 noch nicht geändert hat (so schnell schießen die Preußen nicht), weist die rechte Seite von C1 eine negatives Potential von ca. -5,3V auf, und damit liegt die Basis von T2 auch dann noch auf negativem Potential, wenn der Taster losgelassen wird. Die Schaltung ist nicht mehr im Normalzustand, sondern im "An"-Zustand, der dadurch definiert ist, dass jetzt an R1 eine Spannung abfällt (praktisch die gesamte Versorgungsspannung).
Durch R2 fließt ein Ladestrom in C1 hinein, dessen rechte Platte dadurch immer positiver wird. Dies ist aber zugleich das Potential für die Basis von T2, das folglich ebenfalls positiver wird; die Spannung vor der Basis steigt also von ca. –5,5V auf immer weniger negativere und schließlich auch absolut positive Werte, bis schließlich die Schleusenspannung von +700mV erreicht wird, bei der der Transistor durchsteuert.
Dadurch liegt der Kollektor praktisch wieder auf Emitterpotential, die Basis von T1 sieht keine Vorspannung mehr, und der Transistor T1 sperrt wieder.
T1 verbleibt im gesperrten Zustand - was sollte sich ändern? T2 leitet und leitet, die Basis von T1 sieht keine Spannung, also sperrt T1, und so bleibt es solange, bis man entweder die Versorgungsspannung abschaltet oder bis erneut ein negativer Puls auf die Basis von T2 gegeben wird.
Daher heißt die Schaltung monostabile Kippstufe oder Monoflop: nur der Zustand mit sperrendem Transistor T1 (kein Spannungsabfall an R1). Nur durch einen externen Puls kann die Schaltung in den "An"-Zustand gebracht werden (Versorgungsspannung fällt an R1 ab), und auch nur solange, bis C1 über R2 wieder aufgeladen ist.
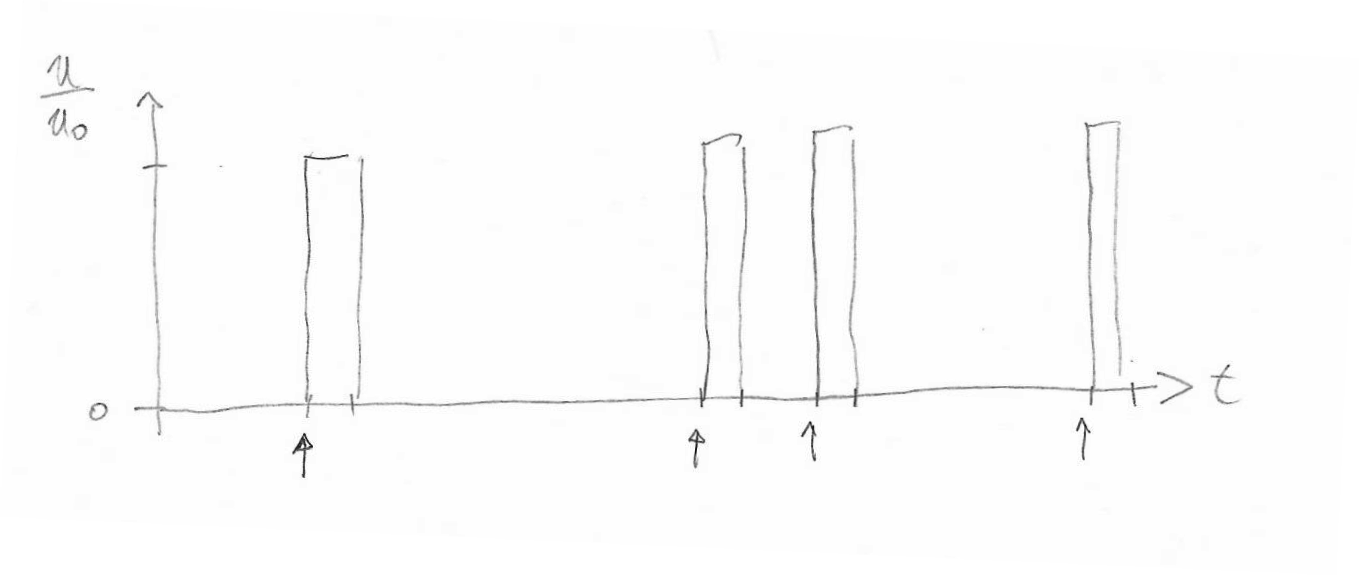
Die Dauer des instabilen Zustands der abgebildeten Schaltung nennt man die Haltezeit \(t_H\)): \begin{equation} t_H = \ln 2 \cdot {\rm R_2 C_1}. \end{equation} Offenbar können wir die monostabile Kippstufe als Einzelpuls-Rechteckgenerator verwenden. Immer wenn wir einen Puls auf den Eingang geben, antwortet die Schaltung mit einem Puls, dessen Breite wir durch Wahl des RC-Gliedes variieren können. Den Startpuls bezeichnet man auch als "Trigger". Eine willkürliche Abfolge von erzeugten Einzel-Rechteckpulsen ist in der Abb. 8-9 gezeigt.
Monoflops werden von vielen Herstellern als integrierte Schaltung angeboten; sie werden vor allem eingesetzt, um eine bestimmte zeitgesteuerte Verzögerung innerhalb eines Stromkreises zu erzeugen. Daher können sie im Allgemeinen als Zeitgeber oder als Impulsdetektoren in elektronischen Geräten eingesetzt werden.
Es gibt zwei Arten von monostabilen Kippstufen, die man als integrierte Schaltung kaufen kann: Nachtriggerbare monostabile Kippstufen bleiben im instabilen Zustand bei wiederholter Anwendung des Triggerimpulses (die Uhr startet erneut). Nicht nachtriggerbare monostabile Kippstufen sind von weiteren Triggerimpulsen unbeeinflusst und bleiben nur für den vorgegebenen Zeitraum im instabilen Zustand (die Uhr wird nicht neu gestartet, zusätzliche Triggerpulse im instabilen Zustand sind ohne Auswirkung).