
Messen in der Chemie
2. Vorlesung
Unter dem Fehler einer Größe wollen wir die Ungenauigkeit dieser Größen verstehen. Der Ausdruck »Fehlerrechnung« bedeutet nichts anderes als Genauigkeitsanalyse. Der Ausdruck »Fehler« kann sich sowohl auf Messgrößen beziehen als auch auf Größen, die aus Messgrößen erschlossen werden.
Absoluter und relativer Fehler.— Wir unterscheiden den absoluten Fehler \(\Delta M\) einer Messgröße \(M\) und den relativen Fehler \(\delta M\) dieser Messgröße.
Der absolute Fehler \(\Delta M\) einer Messgröße M (es wird stets ein großes griechisches \(\Delta\) verwendet) hängt eng mit dem bereits besprochenen Ungenauigkeitsintervall zusammen, innerhalb dessen der Messwert liegt; die beiden Größen unterscheiden sich nur um den Faktor Zwei. \(\Delta M\) weist dieselbe Einheit wie die Messgröße auf. Beträgt die Messgröße z.B. \(U=100\;{\rm V}\) und ist die Messungenauigkeit gleich \(1\;{\rm V}\), so ist diese Ungenauigkeit gleich dem absoluten Fehler der Messung; es ist also \(\Delta U = 1\;{\rm V}\), und wird schreiben:
\[ U = \left(100 \pm 1\right)\;{\rm V}. \]
Das gesamte Fehlerintervall links und rechts vom Messwert \(U=100\;{\rm V}\) beträgt \(2 \Delta U\) und ist daher doppelt so groß wie der absolute Fehler.
Der relative Fehler \(\delta M\) der Messgröße (es wird stets ein kleines griechisches \(\delta\) verwendet) ist gleich dem Quotienten aus dem absoluten Fehler und dem Messwert. Im gegebenen Beispiel (\(U=100\;{\rm V},\; \Delta U = 1\;{\rm V}\)) gilt für den relativen Fehler \(\delta U\):
\[ \delta U = \frac {\Delta U}{U} = \frac{1\;{\rm V}} {100\;{\rm V}} = 0,01 = 1\%. \]Der relative Fehler \(\delta M\) wird häufig als Prozentzahl angegeben. Wir schreiben also:
\[ U = 100\;{\rm V} \pm 1\%. \]Von Geräteherstellern wird der absolute Fehler häufig in Prozent des Messbereiches angegeben. Beträgt dieser z.B. für ein Spannungsmessgerät (Voltmeter) 1% des Messbereiches, dann ist der absolute Fehler im Bereich 0–10 V gleich 100 mV, im Bereich 0–100 V aber gleich 1 V.
Bitte beachten Sie, dass die relative Auflösung gerade umgekehrt definiert ist.
Wenn ein Messwert \(M\) nur innerhalb eines gewissen Intervalls \(\Delta M\) gegeben ist, dann können auch aus \(M\) abgeleitete Größen \(G\) nur innerhalb eines Intervalls \(\Delta G\) genau sein. Wenn eine Messgröße \(M\) fehlerbehaftet ist, dann ist eine Größe \(G\), die aus ihr errechnet wird, ebenfalls fehlerbehaftet.
Wir fragen nun nach dem Zusammenhang von \(\Delta M\) und \(\Delta G\).
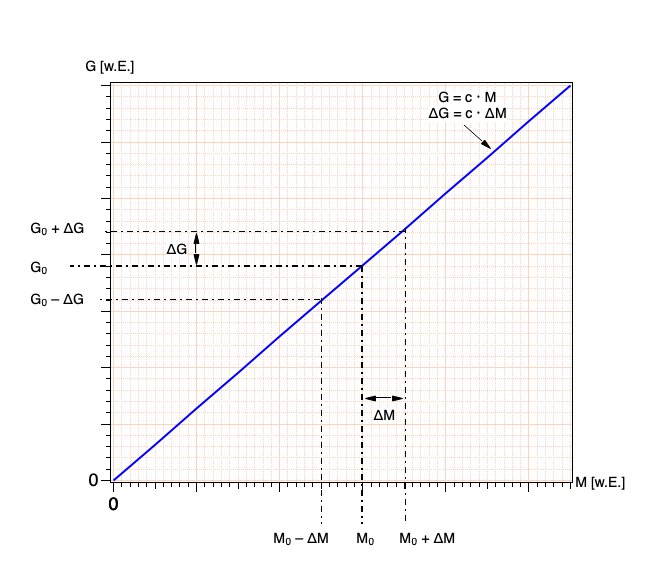
Wie groß das Intervall \(\Delta G\) ist, hängt vom funktionalen Zusammenhang zwischen \(M\) und \(G\) ab. Wir betrachten zunächst den einfachen linearen Zusammenhang: \[ G = c \cdot M \]Der absolute Fehler in \(G\) ist \(c\) mal so groß wie der absolute Fehler in \(M\).
Grundsätzlich kann die Steigung \(c = \frac{\Delta G}{\Delta M}\) auch negativ sein. In der Fehlerrechnung bleibt dies unberücksichtigt. Wir rechnen hier grundsätzlich mit den Beträgen, auch wenn wir dies nicht immer in den Gleichungen ausdrücken, damit sie nicht zu kompliziert aussehen.
In der folgenden Abbildung sind die Zusammenhänge graphisch dargestellt:

Relativer Fehler: Wir teilen nun die Gleichung \(\Delta G = c \cdot \Delta M\) durch die Gleichung \(G = c \cdot M\). (Gleichungen kann man durcheinander teilen, in dem man die linken Seiten und die rechten Seiten durcheinander teilt. Das ist eine sehr häufig verwendete Technik.) Dann finden wir: \[ \frac{\Delta G}{G} = \frac{c \cdot \Delta M}{c \cdot M} \] und nach Kürzen: \begin{equation*} \frac{\Delta G}{G} = \frac{\Delta M}{M}. \end{equation*} Dies wird abgekürzt wie folgt ausgedrückt: \[ \delta G = \delta M. \] Der Ausdruck \(\delta G\) wird auch als relativer Fehler in \(G\) bezeichnet.
Die Beziehung \(\Delta G = c \cdot \Delta M\) gilt auch dann, wenn der lineare Zusammenhang zwischen \(G\) und \(M\) eine additive Konstante aufweist, wenn also die Beziehung lautet: \[ G = c \cdot M + k. \] Denn auch dann gilt \(\frac{\Delta G}{\Delta M} = c\), weil additive Konstanten beim Differenzieren wegfallen.
Für Zusammenhänge der Form \(G = c \cdot M + k \) sind die relativen Fehler \(\delta M\) und \(\delta G\) einander aber nicht gleich. Teilen wir nämlich die Gleichungen \(\Delta G = c \cdot \Delta M\) und \(G = c \cdot M + k \) durcheinander, so erhalten wir:
\[ \frac{\Delta G}{G} = \frac {c \cdot \Delta M}{c \cdot M + k}, \] und wir können für den Fall \(k \neq 0\) nicht kürzen. Das ist immer dann der Fall, wenn die Gerade nicht durch den Nullpunkt (0,0) geht.Folgefehler komplizierterer mathematischer Zusammenhänge.– Wenn der Zusammenhang zwischen der Messgröße \(M\) und der daraus zu ermittelnden Zielgröße \(G\) komplizierter ist, können wir für die Zwecke der Fehlerrechnung eine sehr einfache Näherung nutzen, die auf der sogenannten Taylor-Entwicklung beruht. Die Taylor-Entwicklung ist eine im allgemeinen unendliche Reihe.
Sie dürfen jetzt nicht erschrecken. Die Sache ist nämlich viel einfacher, als sie zunächst aussieht.
Wenn der Zusammenhang zwischen \(M\) und \(G\) komplizierter ist, dann ist der entsprechende Funktionsgraph gekrümmt. Die folgende Abbildung veranschaulicht die Verhältnisse.
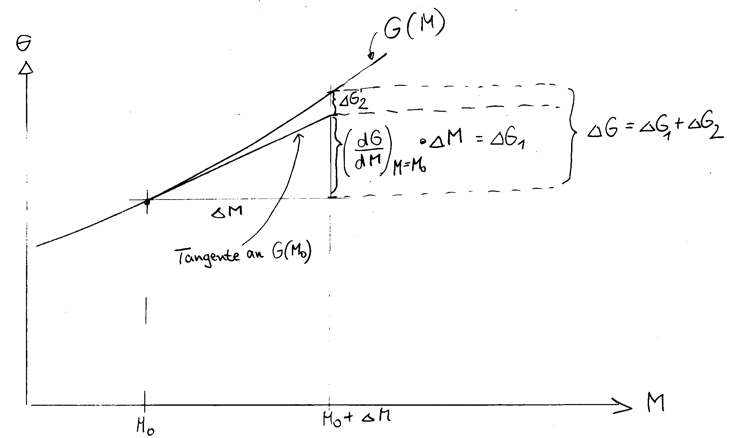
Wenn \(G\) eine Funktion von \(M\) ist und sich \(M\) von \(M_0\) auf (\(M_0 +\Delta M\)) ändert, dann ändert sich \(G\) von \(G_0\) (das ist der Wert von \(G\) an der Stelle \(M=M_0\) auf \(G_0 + \Delta G\). Der Zusammenhang lautet wie folgt:
\begin{equation}\label{eqTaylor} G(M_0 + \Delta M) = G(M_0) + \left[\frac{1}{1!} \cdot \left(\frac{{\mathrm d}G}{{\mathrm d}M}\right)_{M=M_{0}}\Delta M\right] + \left[\frac{1}{2!} \cdot \left(\frac{{\rm d^2}G}{{\rm d}M^2}\right)_{M=M_{0}} \left(\Delta M\right)^2\right] + \left[\frac{1}{3!} \cdot \left(\frac{{\rm d^3}G}{{\rm d}M^3}\right)_{M=M_{0}} \left(\Delta M\right)^3\right] + \left(\ldots\right) \end{equation}
Der Ausdruck \( \left(\frac{{\mathrm d}G}{{\mathrm d}M}\right)_{M=M_{0}} \) bedeutet: die erste Ableitung von \(G\) nach \(M\) and der Stelle \(M=M_{0}\). Die Funktion \(G\) ist ja gekrümmt; ihre Steigung ändert sich mit dem Wert von \(M\).
Für die Zwecke der Fehlerrechnung ist es gewöhnlich ausreichend, in dieser Reihe alle Glieder zu vernachlässigen, die höhere Ableitungen enthalten (also die zweite, dritte usw. Ableitung). Wir berücksichtigen also außer \(G(M_0)\) nur den Term, der die erste Ableitung enthält; wir brechen die Taylor-Reihe nach dem in \(\Delta M\) linearen Term ab. Man nennt dies auch eine Linearisierung. Wir linearisieren also \(G\) in der Umgebung von \(M_{0}\). Wir bedenken außerdem noch, dass \(\frac{1}{1!}=1\) ist und erhalten:
\[ G(M_0 + \Delta M) \approx G(M_0) + \left(\frac{{\mathrm d}G}{{\mathrm d}M}\right)_{M=M_{0}} \cdot \Delta M. \] Umstellen der Gleichung liefert, wenn wir ab jetzt das Gleichheitszeichen statt des Ungefähr-Zeichens verwenden: \[ G(M_0 + \Delta M) - G(M_0) = \left(\frac{{\mathrm d}G}{{\mathrm d}M}\right)_{M=M_{0}} \cdot \Delta M \]Die linke Seite dieser Gleichung, also \( G(M_0 + \Delta M) - G(M_0) \) stellt die Änderung von \(G\) dar, wenn sich \(M\) auf \(M + \Delta M\) ändert. Sie stellt also \(\Delta G\) dar.
In der Messtechnik interpretieren wir \(\Delta M\) als den absoluten Fehler der Messgröße \(M\) und \(\Delta G\) als den absoluten Fehler der Größe \(G\), die mit \(M\) in einem mathematisch definierten funktionalen Zusammenhang steht. In der Mathematik bezeichnet \(\Delta G\) eine Änderung von \(G\). In der Messtechnik interpretieren wir diese Änderung (also \(\Delta G\)) als den Fehler von \(G\). \begin{equation} \label{eqTaylorFehler} \Delta G = \left(\frac{{\rm d}G}{{\rm d}M}\right)_{M=M_{0}} \cdot \Delta M . \end{equation}
Dies ist eine sehr wichtige Beziehung. In Worten lautet sie:
Beispiel: Eine Größe \(G\) entspreche dem Quadrat einer Messgröße \(M\): \begin{equation} \label{eqSquare} G = M^{2} \end{equation}
und \(M\) weise die Ungenauigkeit \(\Delta M\) auf.
Für die erste Ableitung von \(G\) nach \(M\) gilt:
\[ \frac{{\rm d} G}{{\rm d}M} = \frac{{\rm d} M^2}{{\rm d}M} = 2\cdot M. \] Dann gilt nach Gleichung \ref{eqTaylorFehler}: \begin{equation} \label{eqSquareError} \Delta G = 2M \cdot \Delta M. \end{equation}
Der Fehler in \(G\) ist \(2M\) mal so groß wie der Fehler in \(M\).
Wir können dies noch formal etwas bequemer handhaben: wir trennen den Differentialquotienten formal auf, indem wir dessen Nenner auf die rechte Seite schreiben und dann die \({\rm d}\)-Symbole jeweils durch \(\Delta\) ersetzen:
Anwendung: Eine quadratische Fläche \(a\) hat die Seitenlänge \(x = \left(1 \pm 0,1\right)\;{\rm m}.\) Wie groß ist der Fehler der Fläche?
Lösung:
(a) Wir berechnen die Fläche \(a\) aus dem Wert von \(x\): \[a = x^2 = 1\;{\rm m}^2.\]
(b) Wir berechnen den Fehler in \(a\): \begin{align*} a &= x^2\\ \frac{{\rm d}a}{{\rm d}{x}} &= 2x\\ {\rm d} a &= 2x \cdot {\rm d}x\\ \Delta a &= 2x \cdot \Delta x\\ \Delta a &= 2 \cdot 1\;{\rm m} \cdot 0,1\;{\rm m}\\ &= 0,2\;{\rm m}^2 \end{align*}
(c) Wir fassen beides zusammen: die Fläche des Quadrates beträgt \(\left(1 \pm 0,2\right)\;{\rm m}^2\).
Der relative Fehler von \(G = M^2\) ergibt sich durch Teilen der beiden Gleichungen \ref{eqSquareError} und \ref{eqSquare}: \[ \frac{\Delta G}{G} = \frac{2 M \Delta M}{M^{2}} = 2 \frac{\Delta M}{M}. \] Damit erhalten wir: \begin{equation} \label{eqRelSquareErr} \delta G = 2 \cdot \delta M. \end{equation}
Beachten Sie bitte, dass der Faktor \(2\) auf der rechten Seite der Gleichung \ref{eqRelSquareErr} dem Exponenten in Gl. \ref{eqSquare} entspricht.
Dies lässt sich verallgemeinern auf den Fall, dass der Exponent (n) beträgt:
\begin{equation}\label{eqPotenz} G = M^{n} \end{equation} Unsere Näherung liefert sofort: \[ \Delta G = n \cdot M^{n-1} \Delta M \] Division ergibt: \[ \frac{\Delta G}{G} = \frac{n \cdot M^{n-1} \cdot \Delta M}{M^{n}} = n \cdot \frac{\Delta M}{M}, \] also \begin{equation} \delta G = n \cdot \delta M \end{equation} Ist eine Größe \(G\) als \(n\)-te Potenz einer Messgröße \(M\) gegeben, so ist der relative Fehler \(\delta G\) \(n\) mal so groß wie der relative Fehler in \(M\).Bisher haben wir den Fall betrachtet, dass eine zu berechnende Göße \(G\) von einer fehlerbehafteten Messgröße \(M\) abhängt und diese Abhängigkeit in einer mathematischen Gleichung ausgedrückt werden kann.
Eine zu ermittelnde Größe kann aber auch von mehreren Messgrößen abhängen; dies ist in der Praxis fast immer der Fall.
Beispiel: Die Heizleistung \(P\), die einen elektrischen Widerstand \(R\) aufheizt, wenn an ihm eine Spannung \(U\) anliegt, ist durch den Ausdruck
\begin{equation}\label{eqHeizleistung} P = \frac {U^2}{R} \end{equation} gegeben. Wenn wir \(U\) nur bis auf einen Fehler \(\Delta U\) und \(R\) nur bis auf einen Fehler \(\Delta R\) genau kennen, wie groß ist dann der Fehler \(\Delta P\) ?Zur Beantwortung dieser Frage müssen wir uns mit einer speziellen mathematischen Technik beschäftigen, die man partielles Ableiten nennt. Für diejenigen Teilnehmer, die dies noch überhaupt nicht kennen, wird das Konzept der partiellen Ableitung nachfolgend an einem Beispiel vereinfachend erklärt. Wir behandeln das Thema nur so weit, wie wir es im Folgenden wirklich brauchen.
Falls Sie sich mit partiellen Ableitungen bereits auskennen, können Sie diesen Einschub überschlagen.
Viele Größen in der Physikalischen Chemie hängen nicht nur von einer, sondern gleich von mehreren Größen ab.
Beispiel: Das Volumen eines idealen Gases hängt von der Stoffmenge \(n\), der Temperatur \(T\) und dem Druck \(p\) ab (außerdem tritt noch die allgemeine Gaskonstante \(R\):
\begin{equation}\label{eqIdealesGas} V = \frac{nRT}{p}. \end{equation}Ändert sich eine der Größen auf der rechten Seite der Gleichung, dann ändert sich entsprechend auch die linke Seite, also das Volumen \(V\). Ändern sich gleich mehrere Größen auf der rechten Seite, dann ändert sich \(V\) mit jeder dieser Größen. Dabei kann sogar eine Kompensation auftreten; beispielsweise wird \(V\) mit wachsendem \(T\) größer, mit wachsendem Druck \(p\) aber kleiner. Es kann also unter Umständen vorkommen, dass das Volumen gleich bleibt, obwohl sich \(T\) und \(p\) beide ändern. Die Summe beider Änderungen kann sich aufheben.
Wenn wir einmal kurz annehmen, dass \(n\) und \(p\) konstant bleiben und sich nur \(T\) ändert, dann ist \begin{equation} \label{eqODGas} \frac{\diff V}{\diff T} = \frac{nR}{p}, \end{equation} wobei \(\frac{nR}{p}\) nach Voraussetzung eine Konstante ist. Den Ausdruck \(\frac{\diff V}{\diff T} \) können wir hier getrost als einen Bruch auffassen (obwohl dies mathematisch nicht ganz
korrekt ist; nach moderner Auffassung handelt es sich um einen Grenzwert). Wir können den Bruch also trennen und schreiben:
In Worten: Die Änderung in \(V\) ist \(\frac {nR}{p} \) mal so groß wie die Änderung von \(T\).
oder auch, indem wir Gl. \ref{eqODGas} verwenden: \begin{equation} \diff V = \left(\frac{\diff V}{\diff T}\right)_{n,\;p} \cdot \diff T. \end{equation}Hier haben wir die Größe \(\frac{\diff V}{\diff T}\) in eine Klammer gesetzt, und \(n\) und \(p\) als Index rechts unten an die Klammer angefügt, um auszudrücken, dass diese Größen hier konstant bleiben und die Änderung \(\diff V\) nicht beeinflussen.
Sind nun aber alle Größen \(n\), \(T\) und \(p\) veränderlich (und nicht nur \(T\)), dann schreiben wir für die Gesamtänderung \(\diff V\) die Summe der Einzeländerungen von \(V\) mit jeder Größe: \begin{equation}\label{eqPartialDerivative} \diff V = \left(\frac{\partial V}{\partial T}\right)_{n,\;p} \diff T + \left(\frac{\partial V}{\partial n}\right)_{T,\;p} \diff n + \left(\frac{\partial V}{\partial p}\right)_{n,\;T} \diff p. \end{equation} Die in Klammern gesetzten Größen wie z.B. \(\left(\frac{\partial V}{\partial T}\right)_{n,\;p} \) nennen wir partielle Ableitungen. Wir leiten z.B. \(V\) partiell nach \(T\) ab und halten dabei \(n\) und \(p\) konstant. Das ist das Entscheidende bei partiellen Ableitungen. Die anderen Größen werden als Konstanten behandelt. Um sie von normalen Ableitungen zu unterscheiden, verwenden wir das Zeichen \(\partial\) statt eines \(\diff\). Als Index stehen an den Klammern immer diejenigen Größen, die jeweils konstant zu halten sind. Die Summe auf der rechten Seite von Gl. \ref{eqPartialDerivative} nennen wir das totale Differential von \(V\).Partielles Ableiten ist ganz einfach: wollen wir \(\left(\frac{\partial V}{\partial T}\right)_{n,\;p} \) berechnen, so leiten wir \(V\) nach \(T\) ab, halten die anderen Größen konstant und beachten Gl. \ref{eqIdealesGas}:
\[ \left(\frac{\partial V}{\partial T}\right)_{n,\;p} = \frac{nR}{p}. \] Es gibt also gar keine besonderen Rechenregeln dafür. Man muss nur alle anderen Größen konstant halten.Genauso gehen wir auch bei den partiellen Ableitungen nach \(n\) und nach \(p\) vor. wir erhalten dann: \[ \diff V = \frac{nR}{p}\; \diff T + \frac{RT}{p} \; \diff n - \frac{nRT}{p^2} \; \diff p.\] Sie müssen nur die elementaren Ableitungsregeln kennen, und schon können Sie auch partielle Ableitungen bilden.
Das war's schon. Mehr brauchen Sie darüber für unseren Kurs nicht zu wissen. Die dahinter stehende mathematische Theorie ist relativ aufwändig, aber für unsere Zwecke nicht notwendig.
Wir wenden die Technik des partiellen Ableitens nun auf das Problem der Heizleistung an: \[ P = \frac {U^2}{R} \] \begin{equation} \diff P = \left(\frac{\partial P}{\partial U}\right)_R \diff U + \left(\frac{\partial P}{\partial R}\right)_U \diff R. \end{equation}
Wir halten also beim Ableiten von \(P\) nach der Heizspannung \(U\) den Widerstand \(R\) konstant, und beim Ableiten nach dem Widerstand \(R\) die Heizspannung \(U\).
Die Ableitungen sind ganz einfach auszuführen: \begin{equation} \left(\frac{\partial P}{\partial U}\right)_R = \frac{2U}{R}. \end{equation} und \begin{equation} \left(\frac{\partial P}{\partial R}\right)_U = - \frac{U^2}{R^2}. \end{equation}
Das totale Differential lautet also: \begin{equation}\label{eqTotalDiffHeizleistung} \diff P = \frac{2U}{R} \; \diff U - \frac{U^2}{R^2} \; \diff R. \end{equation} Diese Gleichung können wir nutzen, um den Fehler \(\Delta P\) zu bestimmen. Dazu müssen wir mehreren Schritten vorgehen.
Kurzfassung: wir ersetzen in der Fehlerrechnung jedes Differential-d des totalen Differentials durch ein \(\Delta\).
Damit erhalten wir: \begin{equation}\label{eqHeizleistungMaxFehler} \Delta P_{\rm max} = \frac{2U}{R} \Delta U + \frac{U^2}{R^2} \Delta R. \end{equation} Beachten Sie bitte, dass sich das Vorzeichen des zweiten Gliedes auf der rechten Seite umgekehrt hat, weil wir mit den Beträgen rechnen.
Anwendungsbeispiel:
An einem Heizwiderstand \(R = \left(10 \pm 1\right)\;\Omega \) liegt eine Spannung von \(U=\left(100 \pm 5\right)\;{\rm V}\) an. Wie groß ist die Heizleistung?
Lösung:
(1) Wir berechnen den Wert der Heizleistung ohne den Fehler:
\[
P = \frac {U^2}{R} = \frac {100^2\;{\rm V^2}}{10\;\Omega} = 1000\;{\rm W}.
\]
(Anmerkung: es macht nichts, wenn Sie sich mit elektrischen Größen noch nicht so gut auskennen sollten. Wir werden dies später sehr ausführlich besprechen.)
(2) Wir berechnen den maximalen Fehler \(\Delta P_{\rm max}\), indem wir die Werte von \(U\), \(R\), \(\Delta U\) und \(\Delta R\) in die Gl. \ref{eqHeizleistungMaxFehler} einsetzen:
\begin{align*} \Delta P_{\rm max} &= \frac{2 \cdot 100\;{\rm V}} {10\;\Omega} \cdot 5\;{\rm V} + \frac{10^4\;{\rm V^2}}{100\;\Omega^2} \cdot 1\;\Omega.\\ &= 100\;{\rm W} + 100\;{\rm W}\\ &= 200\;{\rm W}. \end{align*}Maximaler und wahrscheinlichster Fehler.
Bisher haben wir den Fehler \(\Delta P\), der aus dem Fehler in \(R\) stammt, und denjenigen, der aus dem Fehler in \(U\) stammt, einfach zahlenmäßig addiert. Diese algebraische oder auch skalare Addition führt auf den maximalen Fehler \(\Delta P_{\rm max}\).
Die skalare Addition zweier Fehler zu einem Gesamtfehler ist in der nachfolgenden Abbildung graphisch dargestellt.
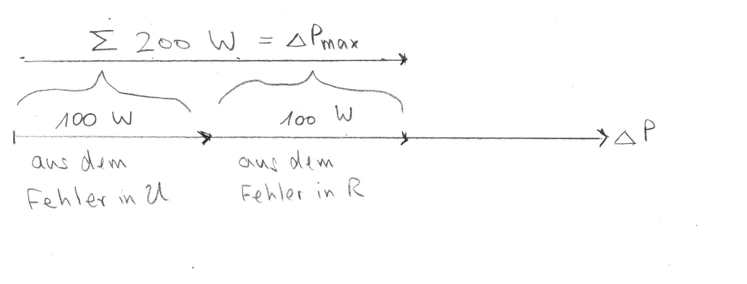
Dabei überschätzt man den auftretenden Gesamtfehler, weil es in Wirklichkeit teilweise auch zu einer Fehlerkompensation kommen kann.
Zur Ermittlung des wahrscheinlichsten Fehlers \(\Delta P\) betrachten wir die Einzelfehler nicht mehr einfach als Zahlen (sogenannte skalare Größen), sondern als Vektoren im Fehlerraum (vgl. die nachfolgende Abbildung).
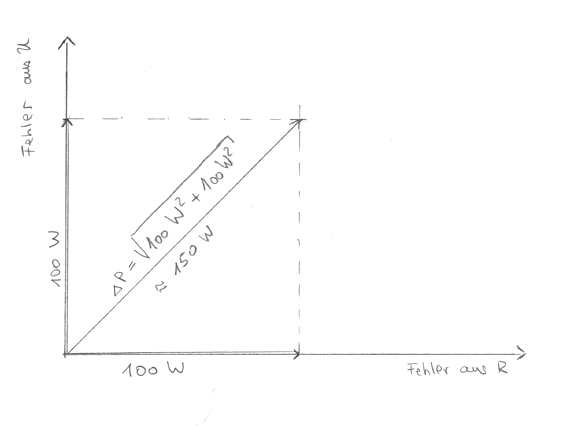
Der Fehlerraum hat gerade so viele Dimensionen, wie unser Gesamtfehler Beiträge aus den einzelnen Messgrößen hat. Im Falle der Leistung \(P\) gibt es zwei Fehlerquellen, nämlich die Spannung \(U\) und den Widerstand \(R\). Daher ist unser Fehlerraum zweidimensional, also eine Fläche. Wenn die Fehler voneinander vollkommen unabhängig sind (die Messung des Widerstandes \(R\) und der Spannung \(U\) also nicht das Geringste miteinander zu tun haben), stehen die Achsen des Fehlerraumes senkrecht aufeinander. Auf jeder Achse des Fehlerraumes wird der jeweilige Teilfehler abgetragen. Der Gesamtfehler ergibt sich durch vektorielle Addition der Teilfehler im Fehlerraum. Da die Achsen senkrecht aufeinander stehen, kann die Länge nach dem Satz des Pytagoras ermittelt werden. Ist \(\Delta P_1\) der Fehler aus der Spannungsmessung und \(\Delta P_2\) der Fehler aus der Widerstandsmessung, so ist (Pytagoreischer Lehrsatz für rechtwinklige Dreiecke!)
\begin{equation}\label{eqFehlerVektor} \Delta P = \sqrt{\Delta P_1^2 + \Delta P_2^2}. \end{equation}Nach dieser Gleichung gilt für unser konkretes Anwendungsbeispiel (die Einheiten lassen wir der Einfachheit halber weg):
\[ \Delta P = \sqrt{100^2 + 100^2} = \sqrt{2 \cdot 100^2} = \sqrt{2}\cdot \sqrt{100^2} = \sqrt{2} \cdot 100 \approx 141. \]Der Fehler \(\Delta P\) ist also deutlich kleiner als \(\Delta P_{\rm max}\).
Weiter unten werden wir sehen, dass wir den Fehler statt auf 141 besser auf 150 runden.
Relativer Fehler bei Größen, die von mehreren Messwerten abhängen.–
Wir betrachten wieder unser Beispiel \(P=\frac{U^2}{R}\).
Wir erinnern uns (siehe Gl. \ref{eqHeizleistungMaxFehler}), dass
\[
\Delta P_{\rm max} = \frac{2U}{R} \Delta U + \frac{U^2}{R^2} \Delta R.
\]
Der relative Fehler \(\delta P_{\rm max}\) ist dann wie folgt gegeben (wir machen das jetzt super-ausführlich Schritt für Schritt zum Nachrechnen; wenn Sie im Bruchrechnen schon Ihr Freischwimmerzeugnis haben, dann übergehen Sie dies bitte):
\[
\delta P_{\rm max} = \frac {\Delta P_{max}}{P} = \frac{\frac{2U}{R} \Delta U + \frac{U^2}{R^2} \Delta R}{\frac{U^2}{R}}\]
Den Ausdruck rechts zerlegen wir in zwei Brüche:
\[
\frac{\frac{2U}{R} \Delta U + \frac{U^2}{R^2} \Delta R}{\frac{U^2}{R}} = \frac{\frac{2U \Delta U}{R} }{\frac{U^2}{R}} +\frac{ \frac{U^2 \Delta R}{R^2}}{\frac{U^2}{R}}
\]
Den Bruch aus zwei Brüchen kann man berechnen, indem man den Bruch im Zähler mit dem Kehrwert des Nenners multipliziert:
\[
\frac{\frac{2U \Delta U}{R} }{\frac{U^2}{R}} +\frac{ \frac{U^2 \Delta R}{R^2}}{\frac{U^2}{R}} = \frac{2U \Delta U}{R} \cdot \frac{R}{U^2} + \frac{U^2 \Delta R}{R^2} \cdot \frac{R}{U^2}
\]
Kürzen:
\[
= 2 \frac{\Delta U}{U} + \frac{\Delta R}{R} = 2 \delta U + \delta R = \delta P_{\rm max}.
\]
Für die einzelnen relativen Teilfehler gelten also dieselben Regeln, wie sie zuvor für Größen angegeben wurden, die nur von einer Messgröße abhängen, und bei multiplikativen Verknüpfungen addieren sich die relativen Fehler.
Hier als weiteres Beispiel die Fehler der Spannung bei gemessenem Widerstand und gemessener Stromstärke gemäß dem Ohmschen Gesetz (bitte nachrechnen!):
\[ U = R \cdot I \] mit \(R\) und \(I\) als Messgrößen und \(U\) als Zielgröße.\[\Delta U_{\rm max} = \frac{\partial U}{\partial R}\cdot \Delta R + \frac{\partial U}{\partial I}\cdot \Delta I = I \cdot \Delta R + R \cdot \Delta I\] \[\delta U_{\rm max} = \frac {\Delta U}{U}\] \[\delta U_{\rm max}= \frac{I \cdot \Delta R}{U} + \frac{R \cdot \Delta I}{U}\] Mit \(\frac{I}{U} = \frac{1}{R}\) und \(\frac{R}{U} = \frac{1}{I} \) folgt: \[\delta U_{\rm max}= \frac{\Delta R}{R} + \frac{\Delta I}{I}\] \[\delta U_{\rm max}= \delta R + \delta I.\] Die relativen Fehler addieren sich, weil die Größen \(R\) und \(I\) multiplikativ verknüpft sind:
Für den wahrscheinlichsten relativen Fehler gilt wieder die vektorielle Addition, so dass: \[ \delta U = \sqrt{(\delta R)^2 + (\delta I)^2}. \]
Zahlenmäßige Angabe eines Fehlers.–
Möglicherweise haben Sie in Ihrem Studium bereits ein Physik-Grundpraktikum an der FU Berlin absolviert. Dort gilt streng die folgende Regel: jeder Fehler wird immer nur 1-stellig angegeben. Das Ergebnis einer Fehlerrechnung wird auf die nächste einstellige Zahl aufgerundet. Für uns würde dies bedeuten, dass wir unser Ergebnis \(\Delta P \approx 141\;{\rm W}\) auf \(200\;{\rm W}\) aufrunden müssten. Bitte beachten Sie, dass wir auf diese Weise den Unterschied zwischen dem maximalen Fehler \(\Delta P_{\rm max}\) und dem wahrscheinlichsten Fehler \(\Delta P\) wieder verlieren würden. So wollen wir daher nicht vorgehen.
Wir geben den Fehler so an, dass die vektorielle Addition der Einzelfehler darin gerade Platz hat. Unser Fehler hat immer die Form:
\[ 1;\; 1,5;\;2;\;2,5;\;3;\;3,5; (\dots);\;8;\;8,5;\;9;\;9,5, \] multipliziert mit der jeweiligen Größenordnung, also zum Beispiel \[ 100;\;150,\;200;\;250\;(\dots). \]Stellen Sie es sich bitte so vor wie in dem folgenden Bild:
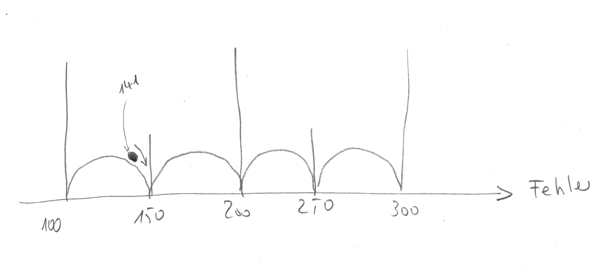
eineinhalbstellig
, weil die erste Stelle jede der Ziffern \(1\dots 9\) annehmen kann, die zweite aber nur den Wert 5. (Halbstelligkeit gibt es übrigens auch bei digitalen Messgeräten. Die meisten Multimeter sind dreieinhalbstellig.)
Angabe von Fehler und Wert zusammen.
Die Zahl der signifikanten Stellen des Wertes und die Höhe des Fehlers müssen zueinander passen. Es dürfen beim Wert nicht mehr Stellen angegeben werden, als der Fehler zulässt.
Beispiel:
Bei der Bestimmung der Faradaykonstanten \(F\) (Einheit \(\frac{\rm C}{\rm mol}\)) im Praktikum aus der Steigung einer Geraden erhält man mit Hilfe einer Auswertesoftware zunächst das Ergebnis:\[ F = \left(95821,341 \pm 2937,23\right)\;\frac{\rm C}{\rm mol}. \]
(a) Wir betrachten zunächst den Fehler. Entsprechend der oben angegebenen Regeln muss der Fehler mit \(\Delta F = 3000\;\frac{\rm C}{\rm mol}\) angegeben werden, denn das ist der nächstgelegene erlaubte Fehlerwert. (Die Nachbarfehler sind 2500 und 3500; diese beiden Fehlerwerte sind weiter von dem Wert 2937,23 entfernt als 3000, unsere Kugel (vgl. Abb. 3) rollt also nach 3000).
(b) Nun betrachten wir den Wert selbst. Da der Fehler im Bereich der Tausender-Stelle liegt, ist die Angabe sämtlicher weiterer Stellen, die im Roh-Resultat auftreten, also die Hunderter, Zehner, Einer usw., physikalisch sinnlos. Ja die Angabe dieser Stellen ist sogar irreführend, denn sie gaukelt eine Genauigkeit vor, die angesichts des Fehlers von \(\Delta F = 3000\;{\rm \frac{C}{mol}}\) gar nicht existiert. Diese Stellen werden nach dem Runden durch Nullen ersetzt, um die richtige Größenordnung anzugeben. Es wird also auf die Tausender-Stelle gerundet. Wir erhalten also auf diese Weise das Endergebnis:
\[ F = \left(96000 \pm 3000\right)\;\frac{\rm C}{\rm mol}. \]Ebensogut könnten wir auch schreiben:
\[ F = \left(96 \pm 3\right)\;\cdot 10^3\;\frac{\rm C}{\rm mol}. \] Die Angabe von zu vielen signifikanten Stellen eines Wertes ist der im PC-Praktikum am meisten gemachte Fehler!Weitere Beispiele: