
Messen in der Chemie
10. Vorlesung
Für Plangitter gilt die folgende Grundregel:
Ein Plangitter muss von parallelem Licht ausgeleuchtet werden.
Das kann man ganz leicht verstehen. Das Gitter strahlt ja nur dann Licht in einen gegebenen Winkel \(\beta\) ab, wenn der Eintrittswinkel \(\alpha\) definiert ist. Wenn viele Lichtstrahlen mit unterschiedlichem Eintrittswinkel das Gitter treffen, dann ergibt sich kein einheitlicher Austrittswinkel \(\beta\). Die Gittergleichung gilt zwar immer noch für jeden einzelnen Lichtstrahl, aber das Gitter ist nicht zum spektralen Auflösen des einfallenden Lichtes verwendbar, weil alle möglichen Austrittswinkel auftreten.
Wir (oder vielmehr der Hersteller des Monochromators) müssen also dafür sorgen, dass parallele Lichtstrahlen auf das Gitter gelangen.
Sonnenlicht ist ein Beispiel für paralleles Licht. Eine Glühlampe ist ein Gegenbeispiel, denn sie emittiert Licht in praktisch alle Richtungen (divergentes Licht).
Die meisten Lichtquellen emittieren divergentes (auseinander laufendes) Licht, das vor der Wechselwirkung mit dem Gitter zunächst parallelisiert werden muss.
In einem Spektrometer (Monochromator) sind zusätzliche optische Komponenten enthalten, die die parallele Ausleuchtung und weitere Abbildungsbedingungen erfüllen.
Zur Änderung der Divergenz (des Auseinanderlaufens) von Licht kann man Linsen und gekrümmte Spiegel verwenden. In Monochromatoren werden Spiegel bevorzugt, weil der Lichtweg bei der Reflexion an Spiegeln nicht von der Wellenlänge abhängt.
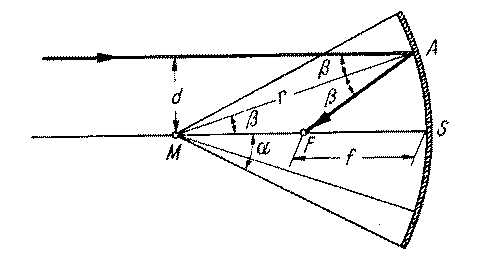
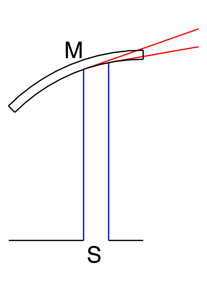
Ein Kugelabschnitt, der auf der Innenseite verspiegelt ist, heißt Hohlspiegel. Abbildung 10-1 zeigt die Abbildungsverhältnisse.

Lichtstrahlen, die parallel zur Hauptachse M-S verlaufen (und hinreichend achsennah sind) heißen Paraxialstrahlen. Für diese gilt:
Paraxialstrahlen werden vom Hohlspiegel in einem Punkt, dem Brennpunkt, vereinigt.
Der Abstand des Brennpunktes vom Scheitel S des Spiegels heißt Brennweite \(f\); für diese gilt: \begin{equation} \boxed{ f=\frac {1}{2}\;r.} \end{equation}
Die Brennweite eines sphärischen Spiegels ist gleich dem halben Kugelradius.
Wegen der grundsätzlichen Umkehrbarkeit der Lichtwege in der Strahlenoptik gilt: Gehen vom Brennpunkt \(F\) Strahlen aus, so werden diese als paralleles Strahlenbündel reflektiert. Damit kann also Licht parallelisiert werden. Voraussetzung ist eine möglichst kleine Lichtquelle im Brennpunkt \(F\). Lichtstrahlen, die von einer ausgedehnten Quelle stammen, kommen nicht alle aus dem Brennpunkt, werden also nicht parallelisiert, und führen damit zu Abbildungsfehlern.
Der Strahlengang in einem Monochromator ist in der Abbildung 10-2 gezeigt. Diese Abbildung ist sehr wichtig.
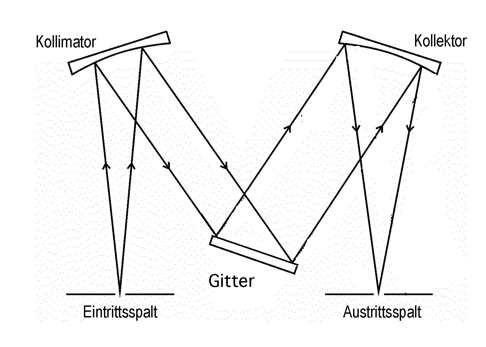
Der Monochromator besteht aus den folgenden Komponenten:
Der Monochromator erzeugt viele Bilder des Eintrittsspaltes, jedes in seiner eigenen Farbe (Wellenlänge). Eines der Bilder gelangt durch den Austrittsspalt. Wenn man in das Innere eines Monochromators schaut, in dessen Eintrittsspalt weißes Licht gelangt, so sieht man in der Umgebung des Austrittsspaltes einen Regenbogen. Ein kleiner Ausschnitt des Regenbogens gelangt durch den Austrittsspalt nach außen. Je kleiner die Öffnungsweite des Austrittsspaltes ist, desto kleiner ist das spektrale Band, das hinausgelangt.
Die Winkeldispersion \(D_\beta = \frac{\rm d\beta}{\rm d\lambda}\) wurde bereits weiter oben erklärt. Sie ist eine Eigenschaft des Gitters allein. Der Einbau des Gitters in einen Monochromator macht es notwendig, eine weitere Größe einzuführen, die lineare Dispersion.
Der Monochromator übersetzt eine vom Gitter herstammende Winkeltrennung \(\Delta \beta\) in eine örtliche Trennung.
Befindet sich der Bildpunkt der optischen Abbildung des Spektrometers im Abstand \(L_B\) vom Gitter (= Länge des 'Austrittsarms' = Abstand Scheitelpunkt des Kollektors vom Austrittsspalt, vgl. Abb. 10-1), dann übersetzt sich die Winkeltrennung \(\Delta \beta\) dort in eine räumliche Trennung \(\Delta x\) zweier Wellenlängen \(\lambda_1\) und \(\lambda_2\). Dies wird in der Abb. 10-3 verdeutlicht.
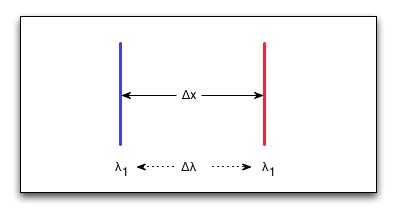
Die 'Aufpunkte' der beiden Wellenlängen \(\lambda_1\) und \(\lambda_1\) unterscheiden sich also um \(\Delta x\) voneinander. Dies wird durch die lineare Dispersion \(D_x\) wiedergegeben.
Die lineare Dispersion \(D_x\) ist definiert als \begin{equation} \label{eqLinDisp} \boxed{D_x = \frac {dx}{d\lambda}.} \end{equation}
Das Symbol für die Winkeldispersion ist \(D_{\beta}\), das Symbol für die lineare Dispersion ist \(D_x\).Abb. 10-4 zeigt die geometrischen Verhältnisse.
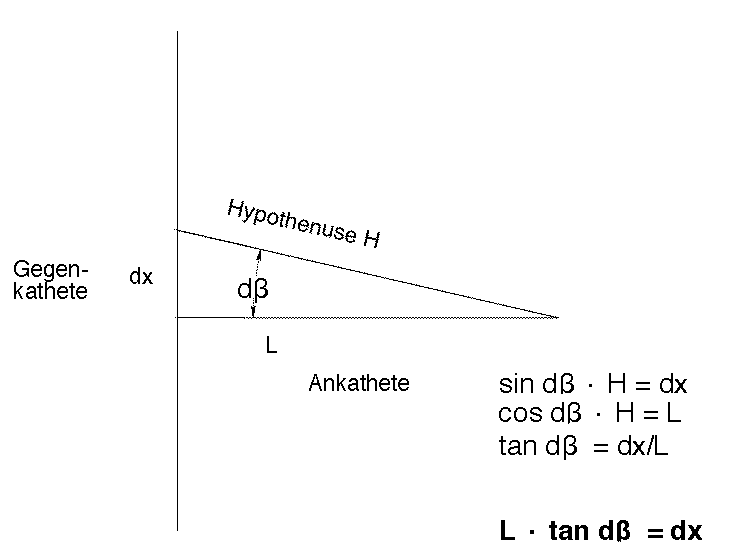
Zwei Strahlen unterschiedlicher Wellenlänge gelangen unter dem Differenzwinkel \(d\beta\) in die Austrittsebene im Abstand \(L_B\) (Austrittsarmlänge, Fokallänge, Ankathete in Abb. 10-4; in dieser Ebene ist der Austrittsspalt). Der Abstand der Aufpunkte (Gegenkathete in Abb. 10-4) beträgt \(\diff x\). Dann ist \begin{equation*} \diff x = \tan \; \diff \beta \cdot L_B \approx \diff \beta \cdot L_B.\ \end{equation*}
Näherungsweise ist \(\tan \varphi \approx \varphi\) für kleine \(\varphi\), denn \(\cos \varphi \approx 1\), \(\sin \varphi \approx \varphi\), \(\tan = \tfrac{\sin}{\cos}\).
Wir multiplizieren jetzt die Gleichung \(\diff x = L_B \cdot \diff \beta\) mit \(\tfrac{1}{\diff \lambda}\) und erhalten: \(\frac {1}{d\lambda}\) multiplizieren: \begin{equation*} {\frac {dx}{d\lambda}= L_B \cdot \frac {d\beta}{d\lambda},} \end{equation*} also mit den Definitionen von linearer Dispersion \(D_x\) und Winkeldispersion \(D_{\beta}\): \begin{equation} \boxed {D_x= L_B \cdot D_{\beta}.} \end{equation}
In Worten: Lineare Dispersion = Austrittsarmlänge \(\times\) Winkeldispersion.
Die Austrittsarmlänge wird auch als Brennweite bezeichnet:
Lineare Dispersion = Brennweite \(\times\) Winkeldispersion.
Bei einem Czerny-Turner-Monochromator ist die Austrittsarmlänge \(L_B\) (Fokallänge) durch den Abstand zwischen dem Scheitelpunkt des Kollektors (Refokussierspiegels) und dem Austrittsspalt gegeben.
Die lineare Dispersion ist zwar formal dimensionslos (Länge/Länge), wird aber gewöhnlich in der Einheit mm/nm angegeben.
Die Umrechnung von m/m in mm/nm ergibt zwischen beiden Einheiten nur einen Zahlenfaktor: \begin{align*} 1 \frac {\rm m}{\rm m} &= \frac {10^3}{10^9} \; \frac {\rm mm}{\rm nm} = 10^{-6} \; \frac {\rm mm}{\rm nm} \end{align*}
Für senkrechten Einfall (\(\alpha\)=0) lässt sich die lineare Dispersion bei Kenntnis der Austrittsarmlänge \(L_B\) und der Gitterkonstante \(G\) mit Hilfe der Gleichungen für die Winkeldispersion wie folgt berechnen: \begin{equation*} D_x = L_B \cdot \frac {kG}{\cos \; \beta}. \end{equation*} bzw. \begin{equation*} D_x = L_B \cdot \frac {kG}{\sqrt{1-(kG\lambda)^2}}. \end{equation*}
Im allgemeinen Fall (\(\alpha \neq 0\)) ergibt sich für die Winkeldisperson
\begin{equation} D_x = L_B \cdot \frac {kG}{\sqrt{1-(kG\lambda - \sin \alpha)^2}}. \end{equation}
(Der zusätzliche Term \(\sin \alpha\) ergibt sich aus der Winkeldispersion für den Fall \(\alpha \neq 0\))
Je länger der Austrittsarm des Monochromators, desto größer ist bei gegebenem Gitter und gegebener Gitterordnung die lineare Dispersion. Es gibt daher 50-cm-Monochromatoren, aber auch 10-m-Monochromatoren. Es gibt allerdings Obergrenzen für die Austrittsarmlänge.
Wenn der Austrittsarm zu lang ist, wirkt das Gitter als Ganzes als
Beugungsscheibchen
. Man kann also keinen 1000-m-Monochromator
bauen, außer man verwendet ein Riesengitter. Die Diskussion dieser
Fragestelltung liegt aber außerhalb des Gesichtskreises dieser Vorlesung. Die größte Austritssarmlänge, von der ich weiß, ist 20 m.
Die Austrittsarmlänge ist durch die Brennweite des Kollektors festgelegt. Man kann auf keinen Fall einfach den Austrittsspalt ein Stück zurücksetzen, um eine höhere lineare Dispersion zu erzielen. Man würde dadurch nur den Monochromator unbrauchbar machen. Die Abbildung würde unscharf, die Wellenlängen würden nicht mehr getrennt (für Experten: die Abbildung wäre nicht mehr konfokal).
Die bisherige Darstellung der spektralen Auftrennung des Lichtes erfolgte ohne Berücksichtigung der Öffnungsbreite \(S\) des
Eintrittsspalts. Wir haben uns den Spalt wird als unendlich schmale Größe vorgestellt. Das führt zur bestmöglichen Abbildung, aber leider kommt kein Licht durch, weil unendlich schmal
heißt nichts weiter, als dass der Spalt geschlossen ist.
Wenn der Eintrittsspalt eine endliche Breite \(S_E\) aufweist (z.B. \(200\;\mu{\rm m}\)), haben parallel aus dem Spalt austretende Strahlen einen unterschiedlichen Strahlengang, je nachdem, wo sie aus dem endlich breiten Spalt austreten (vgl. Abb. 10-5).
Der nachfolgende Gedankengang bereitet den Teilnehmern erfahrungsgemäß Schwierigkeiten. In der realen Vorlesung verbringe ich mit diesem Punkt viel Zeit. Ich versuche, es hier so ausführlich darzustellen, wie es mir möglich erscheint. Bitte ärgern Sie sich nicht, wenn Wiederholungen auftreten.
Entsprechend der linearen Dispersion des Gitters entspricht die
geometrische Breite \(\Delta x\) des monochromatischen Lichtes einem Wellenlängenintervall \(\Delta \lambda\). Dieses
\(\Delta \lambda\) entspricht aber nicht einem realen Wellenlängenbereich der Breite \(\Delta \lambda\), denn es handelt sich ja um monochromatisches Licht, das lediglich im gesamten Wellenlängenbereich \(\Delta \lambda\) vom Monochromator abgegeben wird.
Der Monochromator verhält sich also so, als ob
ihn statt des monochromatischen Lichtes der Wellenlänge \(\lambda\) polychromatisches Licht
mit Wellenlängen zwischen \(\lambda\) und \(\lambda + \Delta \lambda\)
durchlaufen hätte. Es tritt ja nach der gemachten
Voraussetzung nicht wirklich ein Wellenlängenintervall \(\Delta \lambda \)
durch den Monochromator, sondern streng monochromatische Strahlung, die nur
verbreitert erscheint.
Wir schreiben nochmals die Definition der linearen Dispersion auf und verwenden näherungsweise \(\Delta x\) und \(\Delta \lambda\) statt \(\diff x\) und \(\diff \lambda\): \begin{equation*} D_x = \frac {\Delta x}{\Delta \lambda} \end{equation*} Aufgelöst nach \(\Delta \lambda\) ergibt sich: \begin{equation*} \Delta \lambda = \frac {\Delta x}{D_x} \end{equation*} Die Breite \(\Delta x\), mit der monochromatisches (!) Licht durch die unvollkommene Abbildung austrittsseitig erscheint, hängt mit der Spaltbreite wie folgt zusammen (dies folgt aus der Theorie, wir geben dies hier nur an, ohne es herzuleiten): \begin{equation*} \Delta x = \sqrt{2} S. \end{equation*} Damit ergibt sich für \(\Delta \lambda\):
\begin{equation} \label{eqSpaltbreiteAufloesung} \boxed {\Delta \lambda = \frac {\sqrt{2} S}{D_x}.} \end{equation}
Falls die Eintrittsspaltbreite \(S_E\) und die Austrittsspaltbreite \(S_A\) voneinander abweichen, ergibt sich: \begin{equation} \label{eq2Spalte} { \Delta \lambda = \frac {\sqrt{S_E^2 + S_A^2}} {D_x}.} \end{equation} Man erkennt leicht, dass Gl. \ref{eq2Spalte} in Gl. \ref{eqSpaltbreiteAufloesung} übergeht, wenn man \(S_E\) gleich \(S_A\) setzt.
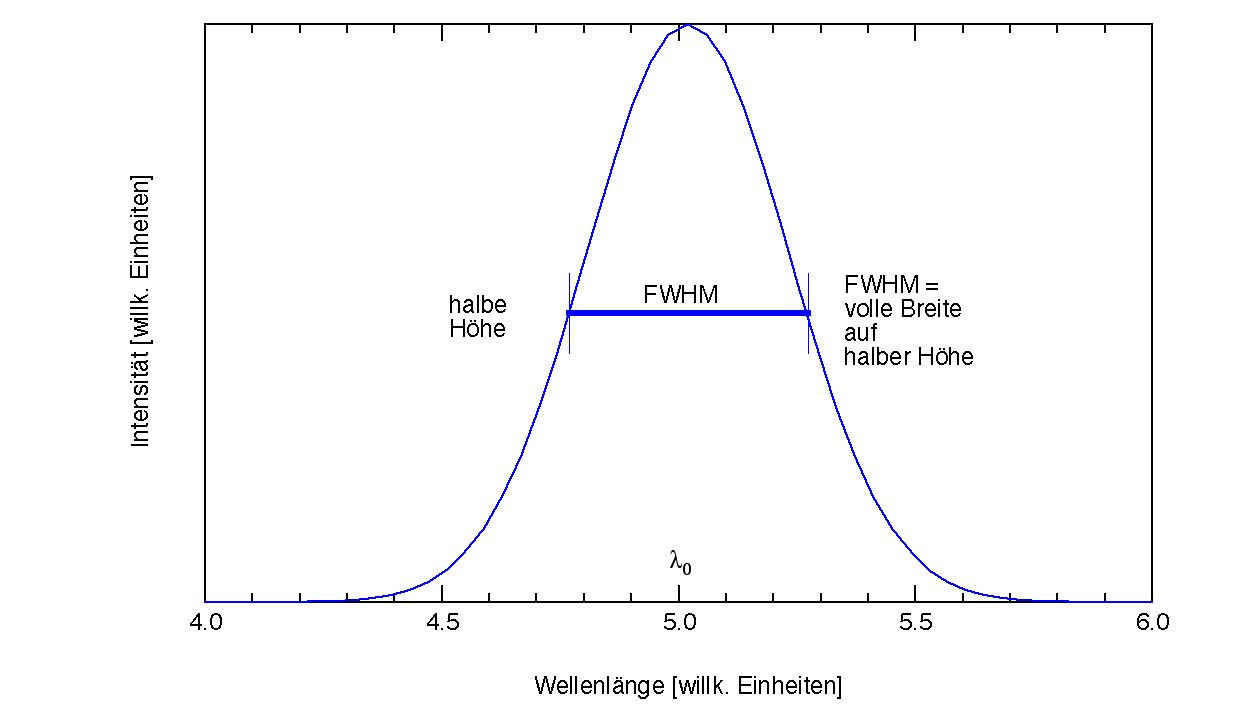
Das vom endlich breiten Spalt erzeugt Profil erweist sich bei näherer Analyse als Gauss-Profil. Die Breite \(\Delta \lambda\) entspricht der vollen Breite auf halber Höhe dieses Profils,vgl. Abb. 10-6.
Die Größe \(\Delta \lambda\) als Resultat der Spaltbreite wird auch als Auflösung des Monochromators bezeichnet.
>aufgelöst.
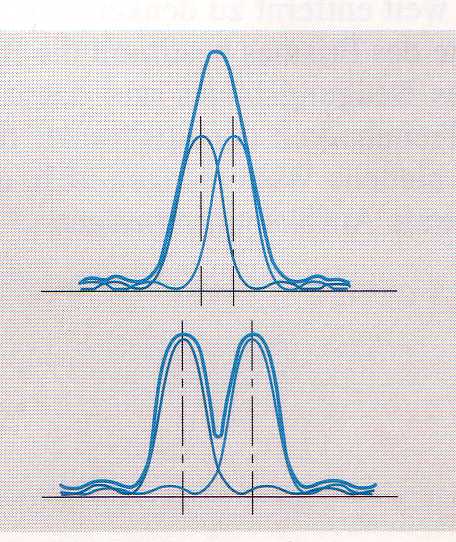
Gleichung \ref {eqResolv} kann man auch wie folgt schreiben: $$ R= k \cdot G \cdot W_G $$ \(W_G\): Ausgeleuchtete Weite des Gitters.
Setzt man in Gl. \ref{eqResolv} den sich aus der Gittergleichung 9-5 ergebenden Ausdruck für \(k\) ein, also \[ k = \frac{\sin \alpha + \sin \beta}{G \cdot \lambda}, \] so erhält man eine praktische Gleichung zur Bestimmung der Auflösung des Gitters bei einer gegebenen Wellenlänge. Es ist dann nämlich \[ R = \frac{N \cdot \left(\sin \alpha + \sin \beta\right)}{G \cdot \lambda}, \] und mit \[ \frac{N}{G} = W: \] \[ R = \frac{W \cdot \left(\sin \alpha + \sin \beta\right)}{\lambda}. \] Setzen wir nun noch \[ \left|\sin \alpha + \sin \beta\right| = 2, \] so erhält man einen Ausdruck für die maximale Auflösung des Gitters zu einer gegebenen Wellenlänge (vgl. Übungsbogen zu dieser Vorlesung).
Das Folgende macht nur Spaß, wenn Sie sich einen Bleistift und ein Blatt Papier nehmen und nachrechnen. Dann ist es aber wirklich ganz lustig.
Sehen Sie sich bitte nochmals die Abb. 10-2 an.
Der Winkel \(\theta\) zwischen unter \(\alpha\) einfallenden und unter \(\beta\) austretenden Lichtes ist beim Czerny-Turner-Monochromator konstant, weil die Position der Spalte festliegt. \(\theta\) und kann vom Anwender in keiner Weise verändert werden. Beide Spiegel sind fest montiert. Das Gitter dreht sich um seine Mittelachse, den Drehwinkel des Gitters nennen wir \(\phi\). Durch die Drehung ändert sich der Eintrittswinkel \(\alpha\). Es gelangt je nach Winkelpositions des Gitters anderes Licht über den Refokussierspiegel zum Austrittsspalt. \(\alpha\) und \(\beta\) sind variabel, aber \(\theta\) nicht. Betrachten Sie jetzt bitte Abb. 10-7.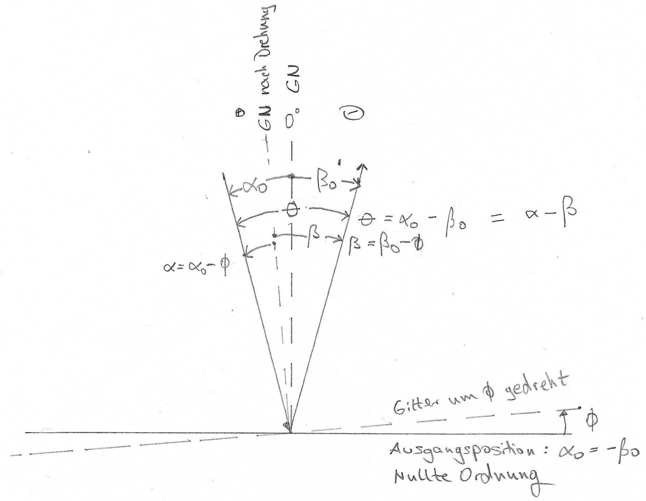
\(\theta\) lässt sich durch \(\alpha\) und \(\beta\) ausdrücken: \begin{equation} \theta = \alpha - \beta. \end{equation}
Lassen Sie sich durch das Minuszeichen nicht verwirren! Bedenken Sie, dass \(\beta\) ein negativer Winkel ist (das Licht tritt rechts von der Gitternormalen aus; es wird in einer negativen Ordnung gemessen).
Wir wiederholen die Gittergleichung: \begin{equation*} \sin \alpha + \sin \beta = kG\lambda. \end{equation*}
Diese ist hier nicht direkt von Nutzen, weil wir weder \(\alpha\) noch \(\beta\) kennen; wir kennen nur \(\theta\) (das sagt uns der Hersteller), und wir kennen \(\phi\) (das Gitter muss uns in irgendeiner Weise sagen, um wieviele Grad es gedreht ist, zum Beispiel durch eine zum Drehwinkel \(\phi\) proportionale Gleichspannung).
Es muss unser Bestreben sein, die Gittergleichung so umzuformulieren, dass \(\theta\) und \(\phi\) darin auftreten statt der Winkel \(\alpha\) und \(\beta\).
Und das geht tatsächlich. Wir bedienen uns einer Mathematik-Formelsammlung. Es ist überraschend einfach.
Es gilt nämlich das Additionstheorem (vgl. Lehrbücher der Mathematik): \begin{equation} \label {Additionstheorem} \sin \alpha + \sin \beta = 2 \cdot \cos \frac {\alpha - \beta}{2}\cdot \sin \frac { \alpha+ \beta}{2} \end{equation} Also auch: \begin{equation} \label{GGL} k\cdot G \cdot \lambda = 2 \cdot \cos \frac {\alpha - \beta}{2} \cdot \sin \frac { \alpha+ \beta}{2} \end{equation}
Wir wissen schon, dass der Ausdruck \(\alpha - \beta\) in Gl. \ref{GGL} gleich dem Gesamtwinkel \(\theta\) ist. Aber was ist \(\alpha + \beta\)?
Der Sinusterm auf der rechten Seite der Gl. \ref{GGL} enthält den Drehwinkel des um seine Achse drehbaren Gitters.
Die Gitternormale zeige zunächst auf \(0^{\circ}\). Die entsprechenden Werte für \(\alpha\) und \(\beta\) sind \(\alpha_0\) und \(\beta_0\). Dreht man das Gitter um den Winkel \(\phi\) gegen den Uhrzeigersinn (es dreht sich dann auch die Gitternormale mit dem Gitter um \(\phi\), und \(\phi\) ist positiv), so ändern sich die Winkel \(\alpha\) und \(\beta\): \begin{align*} \alpha &= \alpha_0 - \phi, \\ \beta &= \beta_0 - \phi, \\ \alpha + \beta &= (\alpha_0 - \phi) + (\beta_0 - \phi) = \alpha_0 + \beta_0 - 2\phi = - 2 \phi, \\ \end{align*} da \(\alpha_0 = - \beta_0\).
Also ist
\begin{equation} \label{alpha_plus_beta} \frac{\alpha + \beta}{2} = -\phi \end{equation}Wir erkennen, dass das Argument des Sinus auf der rechten Seite der Gl. \ref{GGL} bis auf das Vorzeichen gerade gleich dem Drehwinkel \(\phi\) des Gitters ist! Einsetzen in die Gittergleichung liefert (das negative Vorzeichen auf der rechten Seite der Gl. \ref{CTM} kommt aus dem Minuszeichen der rechten Seite von Gl. \ref{alpha_plus_beta}) : \begin{equation} \label{CTM} \boxed{k\cdot G \cdot \lambda = - 2 \cdot \cos \frac { \theta}{2}\cdot \sin {\phi}} \\ \end{equation}
Das ist die Gittergleichung für den Czerny-Turner-Monochromator.
Wir sind aber noch nicht fertig. Wir können noch nutzen, dass \(\theta\) eine Gerätekonstante ist, und setzen \begin{equation} 2 \cdot \cos \frac { \theta}{2} = C, \end{equation} eine Konstante \(C\) des Monochromators. (\(\theta\) ändert sich nie, aber die Wellenlänge, die durchgelassen wird, ändert sich mit dem Gitterwinkel!)
Jetzt lautet die Gittergleichung:
\begin{equation} \label {CTM1} k\cdot G \cdot \lambda = - C \cdot \sin \phi \\ \end{equation}
In kommerziellen Czerny-Turner-Monochromatoren wird das Gitter zu positiven Winkeln gedreht ( gegen den Uhrzeigersinn, \(\phi > 0\)). Wir gelangen am Austrittsspalt in den Bereich negativer Gitterordnungen, zunächst also nach \(k=-1\). In dieser ersten negativen Gitterordnung wird gewöhnlich gemessen.
Hierfür lautet die Gittergleichung (mit \(k=-1\)):
\begin{equation*} -1 \cdot G \cdot \lambda = -C \cdot \sin \phi, \end{equation*} wobei wir das negative Vorzeichen jetzt auf beiden Seiten streichen können, so dass wir erhalten:
\begin{equation} G \cdot \lambda = C \cdot \sin \phi. \end{equation}
Die Beziehung zwischen der durchgelassenen Wellenlänge und dem Gitterwinkel lautet dann: \begin{equation} \label{eqCTM} \lambda = \frac {C}{G} \cdot \sin {\phi}, \end{equation} bzw., wenn man nach dem Winkel zu einer vorgegebenen Wellenlänge fragt: \begin{equation*} \phi = \arcsin \left( \lambda \cdot \frac {G}{C} \right). \end{equation*}
Für den Sonderfall \(\varphi=0\) ergibt sich \(\lambda=0\). Das wäre also formal die Wellenlänge in der ersten Gitterordnung. Es ist dann auch das Produkt \(kG\lambda\) gleich Null. Das Produkt \(kG\lambda\) wird ebenfalls gleich Null, wenn man \(k=0\) setzt. Die optischen Verhältnisse sind dieselben. Der Winkel \(\varphi=0\) entspricht also der Gitterposition für die Nullte Ordnung. Diese Position des Gitters in der Nullten Ordnung entspricht zugleich einer möglichen Kalibrierposition des Gitters für die erste Ordnung, da bei dieser Winkelposition Licht der Wellenlänge 0 nm gemessen würde.
Man kann Gl. \ref{eqCTM} nochmals vereinfachen, in dem man den Sinus durch eine apparative Maßnahme eliminiert. Dies nennt man einen Sinusantrieb; die Abb. 10-8 zeigt Näheres.
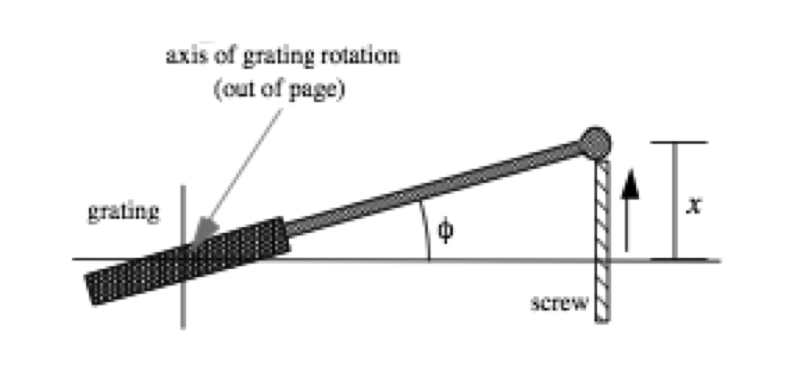
mit der Hypothenuse (Hebelarm) \(H\).
Gl. \ref{eqCTM} lautet damit: \begin{equation*} \lambda = \frac{C}{G} \cdot \frac{x}{H}. \end{equation*}
Für ein gegebenes Gitter mit der Gitterkonstante \(G\), das in den Monochromator verbaut ist, können wir die Konstanten zusammenfassen zu \begin{equation*} K = \frac{C}{G\cdot H} \end{equation*}
Damit ergibt sich für den Monochromator mit Sinusantrieb schließlich die durchgelassene Wellenlänge mit der neuen Konstanten \(K=\tfrac{C}{GH}\) aus der Länge der Schraube: \begin{equation} \lambda = K \cdot x \end{equation}
Ist das nicht unglaublich? Die Gittergleichung \ref{GGL} mit ihren 2 Sinus-Ausdrücken reduziert sich auf eine einfache Geradengleichung zwischen der Wellenlänge und der Länge einer Schraube!
Ebert-Fastie-Monochromator.- Der Ebert-Fastie-Monochromator ist ein einfacher Monochromator, der nur einen sphärischen Spiegel aufweist; dieser ist sowohl für die Kollimierung (= Parallelisierung) als auch für die Refokussierung des Lichtes verantwortlich. Eine Prinzipskizze ist in der Abb. 10-9 gezeigt:
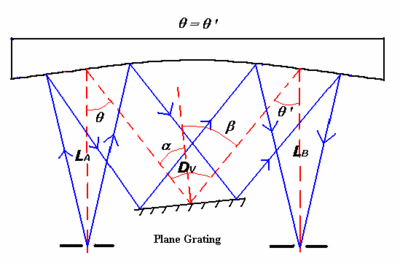
Littrow-Monochromator.- Bei diesem Monochromator gilt \(\alpha = \beta\) (siehe Abbildung 10-10); die Gittergleichung nimmt daher folgende Form an: \[\begin {align*} \sin \alpha + \sin \beta &= kG\lambda\\ \sin \alpha &= \sin \beta\\ 2 \sin \beta &= kG\lambda\\ \to \beta &= \arcsin \frac{kG \lambda}{2}. \end{align*}\]
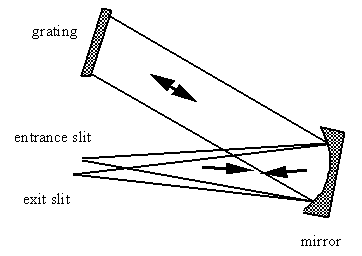
entrance slit) auf einen sphärischen Spiegel. Es wird dann kollimiert und trifft auf das Gitter auf. Es wird dasjenige Licht auf den Austrittsspalt, der unmittelbar neben dem Eintrittsspalt liegt, geschickt, das bzgl. der Gitternormalen denselben Winkel aufweist, d.h. \(\alpha = \beta\).
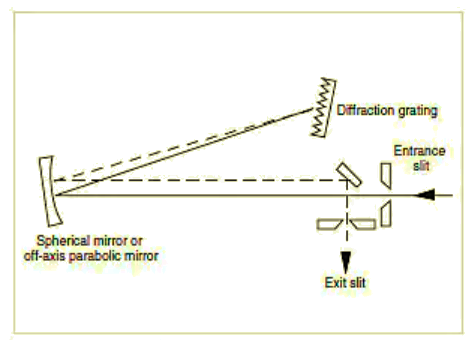
Monochromatoren in Czerny-Turner-, Ebert-Fastie- und Littrow-Konfiguration sind häufig anzutreffende Monochromatortypen, wenn Plangitter verwendet werden. Schreiber dieser Zeilen hat in seiner langjährigen Praxis bisher ausschließlich Czerny-Turner-Monochromatoren kennengelernt, wenn Plangitter verwendet wurden.
Sphärische Gitter.- Bisher haben wir uns mit dem Plangitter, einigen seiner Eigenschaften und mit entsprechenden Monochromator-Konfigurationen beschäftigt. Leider haben Plangitter einen großen Haken: das Licht wird im Monochromator mindestens dreimal reflektiert (Vorspiegel, Gitter, Refokussierspiegel); dies führt zu Reflexionsverlusten durch Absorptionsprozesse an den reflektierenden Oberflächen, und außerdem findet bei jeder spiegelnden Reflexion auch immer ein gewisser Anteil an diffusiver Streuung statt. Die Reflexionsverluste werden dramatisch, wenn wir uns im kurzwelligen Spektralbereich befinden (\(\lambda < 150\;{\rm nm}\)). Die Reflexionsverluste sind bei senkrechtem Auftreffen des Lichtes auf der reflektierenden Oberfläche am größten, so dass man geneigt sein könnte, den Aufbau mit streifendem Lichteinfall zu betreiben; dann sind aber leider die Abbildungsfehler am größten. Die Reflexionsverluste bei senkrechtem Einfall liegen in der Größenordnung von 90%; es wird also nur 10% des auftreffenden Lichtes reflektiert, und wenn insgesamt drei Oberflächen genutzt werden, ist die Gesamtreflektivität \(R\) nur noch gleich \(R=\left(10^{-1}\right)^3 = 10^{-3} = 1 ‰\). Man verliert also praktisch das gesamte Licht.
Zur Lösung dieses sehr ernsten Problems hat man sphärische Gitter ersonnen. Das sind sozusagen sphärische Spiegel mit einer Gitterlinien-Ritzung auf der speigelnden Oberfläche. Sphärische Gitter kombinieren im Grunde die Abbildungseigenschaften sphärischer Spiegel mit den dispersiven Eigenschaften eines Gitters. Man benötigt also keine zusätzlichen Spiegel, um das Licht zu kollimieren und zu refokussieren, das wird alles vom Gitter erledigt. Bei einer Reflektivität des Gitters von 10% erhält man also auch ausgangsseitig 10% der eintretenden Lichtintensität, und nicht lediglich 1 ‰.
Wenn man die Abbildungseigenschaften eines sphärischen Gitters genau berechnen will, dann muss man an jedem Punkt des gekrümmten Gitters die dortige Tangentialfläche anlegen; die Gitternormale steht dann senkrecht auf diese ebene Fläche. Die Rechnungen sind relativ aufwändig; wir wollen sie hier nicht nachvollziehen (weil sie eben nur aufwändig sind, ohne etwas wirklich Neues darzustellen). Aber das Ergebnis wollen wir mitteilen. Dazu betrachten wir die Abbildung 10-12.
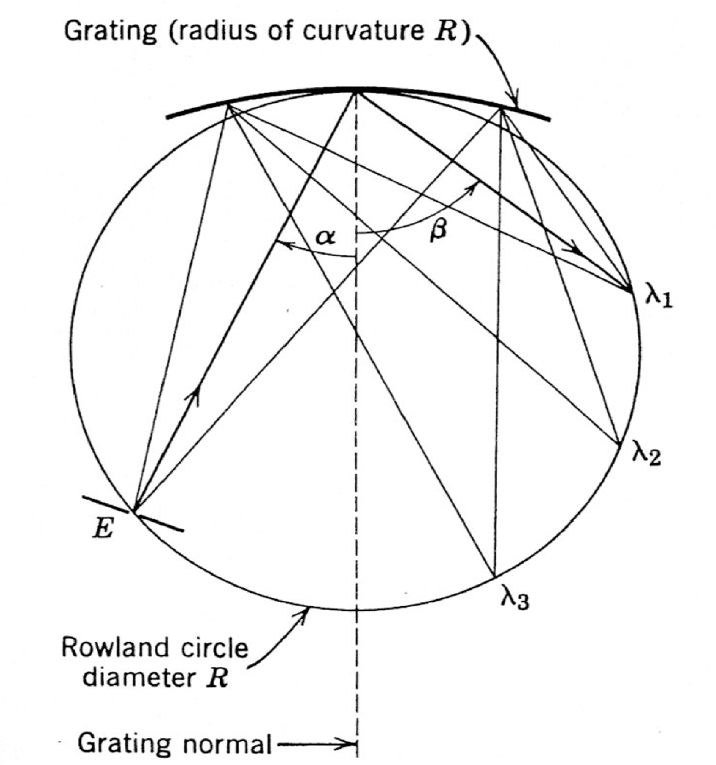
Krümmungsradius), sei \(r\). Dann kann man an das Gitter einen Kreis des Radius \(\frac{r}{2}\) anlegen; dieser ist in der Abb. 10-12 eingezeichnet. Er wird als Rowland-Kreis bezeichnet. Der Rowland-Kreis ist die entscheidende Größe zur Charakterisierung des sphärischen Gitters. Es gilt nämlich (wie gesagt ohne Beweis) die folgende bemerkenswerte Tatsache:
Der Ortspunkt auf dem Rowland-Kreis, auf dem die Fokussierung erfolgt, hängt von der Gitterkonstante \(G\), der Gitterordnung \(k\) und der Wellenlänge \(\lambda\) ab, also von denselben Größen, die auch beim Plangitter auftreten.
Befindet sich der Austrittsspalt an dem Ort, den man durch Spiegelung von \(E\) an der Gitternormalen erhält, so erhält man in der Ruhelage des Gitters (das ist die in der Abb. 10-12 eingezeichnete Lage) am Ort des Austrittsspaltes die Nullte Gitterordnung.
Dreht man das Gitter, dann gelangt man in den Bereich der ersten Gitterordnung und kann das Licht spektral auflösen. Leider dreht sich dabei auch der Rowland-Kreis mit dem Gitter aus seiner Ausgangslage weg; es sind also dann weder Eintrittsspalt noch Austrittsspalt auf dem Rowland-Kreis, so dass die Abbildung unscharf wird. Die Anbieter von Monochromatoren mit sphärischen Gittern haben daher kunstfertige Vorrichtungen ersonnen, die durch eine gleichzeitige Rotations- und Translationsbewegung des Gitters die Unschärfe der Abbildung kompensieren.
Um Abbildungsfehler möglichst klein zu halten, wird das Gitter typischerweise fast senkrecht ausgeleuchtet (Winkel zwischen einfallendem Licht und Gitternormale < 100). Daher heißen entsprechende Monochromatoren in der Fachsprache normal incidence-Monochromatoren (englisch für senkrechter Einfall
), oder kurz NIM. Schreiber dieses hat viele Jahre mit einem NIM gearbeitet und Publikation auf Publikation produziert.
Danke für's Durchhalten!
RF
Statt uns aber in diese Einzelheiten zu vertiefen, wollen wir nun besprechen, worum man sich kümmern muss, damit ein Gitter auch das tut, was es soll. Dies führt geradezu zwingend zu einem weiteren technischen Gerät, dem Monochromator. Er schafft für das Gitter die seinem Zweck entsprechende optische Umgebung.