
Messen in der Chemie
– Sommersemester 2025
1. Vorlesung
Die Lehrbücher der Physik und der Physikalischen Chemie sind beherrscht von Gleichungen, die Beziehungen zwischen Größen regeln. Hier ein paar Beispiele:
\begin{align*} E &= h \nu \\ \\ \Delta G^0 &= \Delta H^0 - T \cdot \Delta S^0 \\ \\ \epsilon &= \epsilon_0 + \frac{RT}{zF} \cdot \ln \frac{a_{\rm ox}}{a_{\rm red}} \\ \end{align*}Wir wollen uns gar nicht weiter mit diesen Gleichungen beschäftigen. Für uns ist hier nur wichtig, dass in ihnen Größen auftreten, die durch irgendwelche mehr oder weniger komplizierten mathematischen Operationen miteinander verknüpft sind. In der ersten der obigen drei Gleichungen sind es die Größen: Photonenenergie \(E\), Plancksche Konstante \(h\) und Frequenz \(\nu\).
Im folgenden wird eine Größe durch das Symbol \(G\) ausgedrückt. \(G\) wird als das Produkt aus einer Maßzahl und einer Einheit aufgefasst:
\begin{equation} \label{eqMasszahlMalEinheit} G = {\color {red}\{G\}} \cdot {\color {blue}[G]}. \end{equation}\(\{G\}\) bezeichnet Maßzahl von \(G\).
\([G]\) ist das Symbol für die Einheit von \(G\).
Zum Beispiel:
Die Frequenz \(\nu\) sei gegeben zu \(\nu\) = 104,6 MHz.
Der Druck \(p\) sei gegeben zu \(p\) = 52357 Pa.
Dann ist gemäß Gl. \ref{eqMasszahlMalEinheit}: \(\{p\} = 52357\) und \([p] = {\rm Pa}\).
Es ist sehr wichtig, einzusehen, dass der Ausdruck 52357 Pa
ein Produkt darstellt. Mit dem Produkt \(\{G\} \cdot [G]\) können Sie rechnen wie mit jedem anderen Produkt auch. Wenn beispielsweise die Größen \(m = 5\;{\rm kg}\) und \(v = 5\;\frac{\rm m}{\rm s}\) vorliegen und Sie das Produkt \(P = m \cdot v\) bilden sollen, dann ist \(P\) gegeben zu
\[ P = \{m\} \cdot [m] \cdot \{v\} \cdot [v] = \{m\} \cdot \{v\} \cdot [m] \cdot [v] \] \[= 5\;{\rm kg} \cdot 5\;\frac{\rm m}{\rm s} = 5 \cdot 5 \cdot {\rm kg} \cdot \frac{\rm m} {\rm s} = 25 \; \frac{\rm kg \cdot m}{\rm s},\]
denn in einem Produkt sind die einzelnen Größen ja vertauschbar, so dass wir umsortieren und die jeweiligen Maßzahlen und Einheiten zusammenfassen können.
Mit dem Produkt \(\{G\} \cdot [G]\) können Sie rechnen wie mit jedem anderen Produkt auch. Wenn beispielsweise die Größen \(m = 5\;{\rm kg}\) und \(v = 5\;\frac{\rm m}{\rm s}\) vorliegen und Sie das Produkt \(p = m \cdot v\) bilden sollen, dann ist \(p\) gegeben zu \[ p = 5\;{\rm kg} \cdot 5\;\frac{\rm m}{\rm s} = 5 \cdot 5 \cdot {\rm kg} \cdot \frac{\rm m} {\rm s} = 25 \frac{\rm kg \cdot m}{\rm s}.\]
| Größe | Symbol | Einheit | Symbol |
| Länge | \(\ell\) | Meter | m |
| Zeit | \(t\) | Sekunde | s |
| Masse | \(m\) | Kilogramm | kg |
| Stromstärke | \(I\) | Ampere | A |
| Temperatur | \(T\) | Kelvin | K |
| Stoffmenge | \(n\) | Mol | mol |
| Lichtstärke | \(I_v\) | Candela | cd |
Abgeleitete SI-Einheiten sind alle Einheiten, die sich aus den Basiseinheiten ohne Verwendung von Zahlenfaktoren ergeben. Wichtige abgeleitete Einheiten erhalten oft selbständige Bezeichnungen mit Namen bedeutender Persönnlichkeiten aus dem Bereich der Naturwissenschaften.
Einheiten, die vom Namen einer Person abstammen, beginnen mit einem Großbuchstaben (Newton → N; Pascal → Pa).
SI-fremde (inkohärente) Einheiten sind solche, die sich aus SI-Einheiten nur durch Umrechnungsfaktoren ungleich Eins umrechnen lassen. Die Ausdrücke "SI-fremd" und "inkohärent" bedeuten dasselbe.
Ein Beispiel ist die Geschwindigkeit in der Einheit km/h: \[{1\;\rm km/h = \frac {1}{3,6}~m/s}\]Der Umrechungsfaktor beträgt \(\frac{1}{3,6} = 0,2777(\dots).\)
Auch solche Einheiten, die sich von einer SI-Einheit um eine Potenz von 10 unterscheiden (außer \(10^0=1\) natürlich), sind inkohärent!
Beispiele:Weiteres zu inkohärenten Einheiten.– Inkohärente Einheiten kommen in der Fachliteratur und im Laboralltag sehr häufig vor. Tatsächlich sind abgeleitete SI-Einheiten etwas, das man am ehesten in (didaktisch aufbereiteten) Lehrbüchern findet. Das häufige Vorkommen inkohärenter Einheiten liegt daran, dass
Betrachten wir als Beispiel die Größe Energie (\(E\)). Ihre SI-Einheit ist das Joule (J), mit \[{\rm 1\;J = 1 \frac{kg \cdot m^2}{s^2} = 1\; N \cdot m.}\]
Im Bereich der Atom- und Molekülphysik (eine der Grundlagen der modernen Chemie!) ist die Einheit Joule ganz unpraktisch, weil die entsprechende Energiemenge von \(1\;{\rm J}\) auf einer molekularen Skala viel zu groß ist. Die typische Energiemenge, die bei einer Reaktion zweier Moleküle miteinander freigesetzt wird, liegt in der Größenordnung \(5 \cdot 10^{-19}\;{\rm J}\). Als "natürliche" Einheit der Energie wird in der Atom- und Molekülphysik sowie in weiten Bereichen der Spektroskopie seit langem das Elektronenvolt (Symbol eV) verwendet. 1 eV entspricht der kinetischen Energie, die ein einzelnes Elektron gewinnt, wenn es über eine Potentialdifferenz von 1 V beschleunigt wird. Die Umrechnung von Joule in Elektronenvolt erfolgt mittels der Beziehung \[{\rm 1\;eV = 1,6022 \cdot 10^{-19}\;J;}\] \[{\rm 1\;J = 6,2414 \cdot 10^{18}\;eV.}\] Die oben genannte Energiemenge bei einer Reaktion zweier Moleküle miteinander beträgt 3 eV; die Ionisierungsenergie des Wasserstoffatoms beträgt ca. 13,6 eV. Wer immerfort mit der Einheit eV rechnet und arbeitet, erlangt ein Gefühl dafür, ob eine molekulare Energiemenge groß oder klein ist, oder ob z.B. ein Rechenfehler vorliegt.
Einheitenvorsätze: Da es oft vorkommt, dass die Grundeinheiten für das praktische Rechnen zu groß oder zu klein sind, werden dezimale Vielfache oder Bruchteile gebildet, die durch Vorsätze gekennzeichnet werden. Die mehrfache Verwendung von Vorsätzen auf eine Einheit ist nicht erlaubt. Dies ist vor allem wichtig für das Kilogramm, das bereits einen Vorsatz enthält. Es ist also KEIN \(\mu\)kg erlaubt. Vorsätze dürfen nur vor das Gramm gesetzt werden, also z.B. ng oder \(\mu\)g. Dies führt oft zu Fehlern, da der Einheitenvorsatz \(\mu\) den Faktor \(10^{-6}\) bezeichnet, aber \(1\;\mu {\rm g} = 10^{-9}\;{\rm kg}\) ist. Wer eine Masse von \(3,5\cdot 10^{-6}\;{\rm kg} \) einer Substanz abwiegen will, kann statt dessen \({\rm 3,5\;mg }\) sagen (und wird es wohl auch tun); auf keinen Fall darf man "\( 3,5\;\mu {\rm kg}\)" dazu sagen.
Die folgende Tabelle gibt die dekadischen Einheitenvorsätze an:| Potenz | Symbol | Name | Potenz | Symbol | Name |
| \(10^1\) | da | Deka | \(10^{-1}\) | d | Dezi |
| \(10^2\) | h | Hekto | \(10^{-2}\) | c | Centi |
| \(10^3\) | k | Kilo | \(10^{-3}\) | m | Milli |
| \(10^6\) | M | Mega | \(10^{-6}\) | \(\mu\) | Mikro |
| \(10^9\) | G | Giga | \(10^{-9}\) | n | Nano |
| \(10^{12}\) | T | Tera | \(10^{-12}\) | p | Piko |
| \(10^{15}\) | P | Peta | \(10^{-15}\) | f | Femto |
| \(10^{18}\) | E | Exa | \(10^{-18}\) | a | Atto |
| \(10^{21}\) | Z | Zetta | \(10^{-21}\) | z | Zepto |
| \(10^{24}\) | Y | Yotta | \(10^{-24}\) | y | Yocto |
Einheitenvorsätze binden stärker an eine Einheit als eine Potenz.
Beispielsweise bedeutet \(26\;{\rm cm}^{2}\): 26 Quadratzentimeter, nicht 26 Zentiquadratmeter: \(26\;{\rm cm}^{2} = 26\;{\rm (cm)^{2}}\) und nicht \(26\;{\rm c(m^{2})}\).
Entsprechend ist \(\mu {\rm m^2} = \left(\mu {\rm m}\right)^{2}\) und nicht \(\mu\left( {\rm m}\right)^{2}\), also Quadrat-Mikrometer, nicht Mikro-Quadratmeter.
Bei der Potenzierung wird also die Einheit (z.B. m
) zusammen mit dem Einheitenvorsatz (z.B. \(\mu\)
) als eine Einheit betrachtet.
\(\mu\)ein Symbol für die Zahl \(10^{-6}\), also ein Faktor; \(\mu{\rm m}\) bedeutet nichts anderes als \(10^{-6}\;{\rm m}\). Die Potenz wirkt aber auch auf diesen Faktor, er wird mitpotenziert. Das ist anders als in der
normalenMathematik: dort bindet die Potenz stärker als ein Vorfaktor: \[ a \cdot b^{\;c} = a \cdot \left( b^{\;c} \right) \] Dagegen gilt bei Einheiten mit Einheitenvorsatz: \[ \mu{\rm m}^2 = \left(10^{-6}\;{\rm m}\right)^2 = 10^{-12}\;{\rm m}^{2}. \]
Die Umrechnung inkohärenter Einheiten ineinander kommt sehr oft vor und muss geübt werden.
Beispiel:
Wieviel Kubiknanometer entsprechen 2 \(\mu {\rm L}\)?
Wir rechnen beide Volumina zunächst in SI-Basiseinheiten um:
\[
2\;\mu{\rm L} = 2 \cdot 10^{-6} \; {\rm L} = 2 \cdot 10^{-6} \;\cdot 10^{-3}\;{\rm m^3} = 2 \cdot 10^{-9}\;{\rm m}^3
\]
\[
1\; {\rm nm}^{3} = 1\; \left({\rm nm}\right)^{3} =\left(10^{-9}\;{\rm m}\right)^{3} = \left( 10^{-9}\right)^{3} \cdot {\rm m}^3 = 10^{-27}\;{\rm m^3}
\]
Wir teilen nun die beiden Gleichungen durcheinander:
\[
\frac{2\;\mu{\rm L} }{1\; {\rm nm}^{3}} = \frac{2 \cdot 10^{-9}\;{\rm m}^3}{10^{-27}\;{\rm m^3}} = 2 \cdot 10^{18}
\]
Wir lösen die Gl. jetzt nach \(2\;\mu{\rm L} \) auf und erhalten:
\[
2\;\mu{\rm L} = 2 \cdot 10^{18} \; {\rm nm^3}.
\]
Eine Größe kann in unterschiedlichen Einheiten ausgedrückt werden. Die Dimension einer Größe ist das, was die unterschiedlichen Einheiten einer Größe miteinander gemeinsam haben.
Beispielsweise kann die Geschwindigkeit \(v\) eines bewegten Körpers wie folgt ausgedrückt werden:
\begin{align*} [v] &= \frac{\rm m}{\rm s}\\ \\ [v] &= \frac{\rm cm}{\rm s}\\ \\ [v] &= \frac{\rm km}{\rm h}\\ \\ [v] &= \frac{\rm nm}{\rm ms}\\ \end{align*}Diese unterschiedlichen Einheiten weisen dieselbe Dimension auf, nämlich Länge/Zeit.
In der Mechanik verwendete Größen beruhen auf den Dimensionen Länge L, Zeit T und Masse M.
Dimensionen werden durch große steile Groteskbuchstaben dargestellt. (Zeichensatz "Arial, "Helvetica" o.ä.).
Die Dimension erhält man aus der Größe formal durch Anwenden des Dimensionsoperators "dim".
Beispiele: \begin{align*} {\rm Geschwindigkeit: dim(}v) &= {\sf L \cdot T^{-1}.}\\ {\rm Dichte: dim}(\rho) &= {\sf M \cdot L^{-3}}.\\ \end{align*} Insgesamt gibt es die folgenden Dimensionen:| Dimension | Symbol |
| Länge | \({\sf L}\) |
| Zeit | \({\sf T}\) |
| Masse | \({\sf M}\) |
| Stromstärke | \(I\) |
| Temperatur | \(\Theta\) |
| Stoffmenge | \({\sf n}\) |
| Lichtstärke | \({\sf I_v}\) |
Größe, Dimension und Einheit dürfen nicht verwechselt werden! Die Masse \(m\) ist eine physikalische Größe; sie hat beispielsweise die physikalische Eigenschaft der Trägheit; die Dimension einer Masse M hat selbstverständlich keine physikalischen Eigenschaften, sondern ist das, was den verschiedenen Einheiten der Masse (wie z.B. Kilogramm, Gramm, usw.) gemeinsam ist. Diesen Einheiten der Masse sind ja nicht die physikalischen Eigenschaften der Masse (wie z.B. Trägheit) gemeinsam, sondern die Dimension M der Masse \(m\).
Die Dimension einer beliebigen Größe \(G\), also dim(\(G)\), lässt sich stets als Produkt aus Potenzen der genannten Dimensionen darstellen: \begin{equation} \label {eqDimension} {\rm dim}(G)= {\sf L}^{\alpha} {\sf M}^{\beta} {\sf T}^{\gamma} {\sf I}^{\delta} \Theta^{\epsilon} {\sf N}^{\zeta} {\sf J}^{\eta} . \end{equation}
Die Exponenten \(\alpha\), \(\beta\) usw. in dieser Gleichung sind im allgemeinen kleine ganze Zahlen.
Da eine Größe mit dem Exponenten Null stets Eins ergibt (\(a^0=1\) für alle \(a \neq 0\)), können die entsprechenden Glieder auch weggelassen werden, und wir erhalten, wie oben angegeben: \({\rm dim}(\rho) = {\sf M \cdot L^{-3}}\), wobei die Reihenfolge der Faktoren auf Konvention beruht.
Dimensionslose Größen und Pseudo-Einheiten.– Dimensionslose Größen sind solche, bei denen alle Faktoren \(\alpha\), \(\beta\) usw. gleich Null sind. Die Dimension ist dann gleich Eins, und man spricht von dimensionslosen Größen.
Dimensionslose Größen weisen keine Einheit auf.
Ein wichtiges Beispiel einer dimensionslosen Größe ist der Winkel \(\vartheta\). Der Winkel ist definiert als die Bogenlänge eines Kreisausschnittes dividiert durch den Radius des Kreises:
\[\rm \vartheta = \frac{\rm Bogenlänge}{\rm Radius}\]
Damit hat der Winkel die Dimension \(\frac{\sf L}{\sf L} = 1.\)
Der Vollkreis hat einen Winkel von \(\frac{2 \pi r}{r} = 2 \pi.\)
Gibt man einen Winkel an, so ist dies also einfach eine Zahl zwischen Null und 2\(\; \pi\), also z.B. \(\vartheta = 0,923\). Der Zahl \(0,923\) sieht man aber überhaupt nicht an, dass sie einen Winkel darstellt. Sie könnte doch sonst irgendetwas sein, z.B. die Wahrscheinlichkeit für das Eintreten eines Ereignisses. Daher ist es üblich, solchen dimensionslosen Größen eine Pseudo-Einheit zuzuordnen, um kenntlich zu machen, worum es sich bei der Zahlenangabe der Sache nach handelt. Im Falle des Winkels verwendet man die Pseudo-Einheit "rad".
"rad" ist nichts weiter als ein Symbol für die Zahl Eins:
\[\rm rad = 1.\]Statt also zu schreiben: \(\vartheta = 0,923\), schreiben wir lieber: \(\vartheta = 0,923\; {\rm rad}.\)
Daneben wird, insbesondere in Alltagszusammenhängen, die Einheit "Grad" verwendet, der als Symbol ein hochgestellter Kreis zugeordnet ist. Die Winkeleinheit Grad ist so festgelegt, dass \(360^{\circ} = 2 \pi.\)
Folglich ist
\[1^{\circ} = \frac{2 \pi\;{\rm rad}}{360} = 0.017453(\dots)\;{\rm rad}\] und \[1\;{\rm rad} = \frac{360^{\circ}}{2\; \pi} = 57,2958(\dots)^{\circ}.\]Die Beziehung zwischen Größen werden durch Gleichungen angegeben.
Hinsichtlich der Verwendung von Einheiten in den Größen unterscheiden wir:
Hier ein Beispiel aus dem Bereich der Akkustik: für die Schallgeschwindigkeit \(c\) in Luft gilt nach Lehrbüchern der Akkustik die Zahlenwertgleichung
\begin{equation*} \label {eqZahlenwert1}
c = 331,6 + 0,6\; t.
\end{equation*}
mit der Geschwindigkeit in \(\dfrac{\rm m}{\rm s}\) und der Temperatur \(t\) in \(^{\circ}\)C.
Da wir die Maßzahl einer Größe \(G\) mit dem Symbol \({G}\) bezeichnen, wäre es formal besser, obige Gleichung wie folgt aufzuschreiben:
\[ \{c\} = 331,6 + 0,6\; \{t\}. \]
So wird es aber normalerweise nicht gemacht.
Die Temperatur wird in dieser der Literatur entnommenen Gleichung mit \(t\) und nicht mit \(T\) bezeichnet. Erwarten Sie besser keine Konsistenz bei der Bezeichnung von Größen in der wirklichen Fachliteratur.
Um die Schallgeschwindigkeit bei 20\(\;^{\circ}\)C zu ermitteln, rechnet man $$c = 331,6 + 0,6 \cdot 20 = 343,6.$$ Man weiß oder hat zu wissen, wie dies zu verstehen ist: diese Zahlenwertgleichung liefert richtige Ergebnisse nur dann, wenn die Geschwindigkeit in \({\rm m/s}\) und die Temperatur in \(^{\circ}\)C gegeben sind.
Zahlenwertgleichungen kommen in der Praxis sehr häufig vor. Das liegt daran, dass in praktischen Zusammenhängen jeder der Beteiligten weiß, welche Einheiten zu verwenden sind. Umgekehrt bedeutet dies, dass jeder aus diesem Zusammenhang ausgeschlossen ist, der nicht die dort verwendeten Einheiten kennt. In gewisser Weise sind Zahlenwertgleichungen etwas für Eingeweihte.
Bei einer zugeschnittenen Größengleichung werden die in der Gleichung auftretenden Größen jeweils durch die Einheit geteilt, in der sie in der Gleichung auftreten.
Teilen wir nämlich eine Größe durch ihre Einheit, so bleibt lediglich der Zahlenwert übrig:
\[ \frac{G}{[G]} = \{G\}.\]
Das bekannte Ohmsche Gesetz \(U=R \cdot I\) hat beispielsweise als zugeschnittene Größengleichung die Form:
\[\frac{U}{\rm V} = \frac{R}{\Omega} \cdot \frac{I}{\rm A} \]
und nimmt bei Verwendung der Einheiten \({\rm kV}\), \({\rm A}\) und \(\Omega\) die folgende Form an:
\[\frac{U}{\rm kV} = 10^{-3}\;\frac{R}{\Omega} \cdot \frac{I}{\rm A}. \]
Weiteres Beispiel: Die Zahlenwertgleichung für die Schallgeschwindigkeit nimmt als zugeschnittene Größengleichung die Form an:
\begin{equation*}
\frac{c}{\left(\dfrac{\rm m}{\rm s}\right)} = 331,6 + 0,6\;t/^{\circ}{\rm C}.
\end{equation*}
Wenn wir etwa \(c\) für \(20\;^{\circ}{\rm C}\) berechnen wollen, kürzt sich die Einheit \(^{\circ}{\rm C}\) weg, uns es verbleibt
\begin{equation*}
c/\frac{\rm m}{\rm s} = 331,6 + 12.
\end{equation*}
Multiplizieren wir jetzt mit der links im Nenner stehenden Einheit, so erhalten wir das Ergebnis:
\[c = 343,6\;{\rm m/s}\]
Wir erhalten hier also das formal korrekte Ergebnis, einschließlich der Einheit.
Beispiel: aus der Definition der Dichte \[\rho = \frac {m}{V}\] folgt die Einheitengleichung \[[\rho] = \left[\frac {m}{V}\right] = \frac {[m]}{[V]} = \frac {\rm kg}{\rm m^3}.\] Einheitengleichungen können mit Vorteil verwendet werden, um herauszufinden, ob eine gegebene Gleichung überhaupt richtig sein kann. Die sich für die linke Seite insgesamt ergebende Einheit muss nämlich mit der sich insgesamt für die rechte Seite ergebenden Einheit übereinstimmen; sonst ist in der Gleichung der Wurm drin.🐛
Ziel der Messung einer Größe \(G\) ist die im Rahmen der praktischen Gegebenheiten möglichst genaue Bestimmung ihrer Maßzahl \(\{G\}\).
Wir machen nun eine Annahme, die (wie wir weiter unten sehen werden) grundsätzlich nicht experimentell bewiesen werden kann:
Wir nehmen also z.B. an, dass die Ruhemasse \(m_e\) des Elektrons einen wahren Wert hat. Wir nehmen weiter an, dass \(m_e\) für jedes beliebige Elektron genau gleich groß ist.
Die Maßzahl der Größe \(m_e\) ist eine ganz bestimmte reelle Zahl. Sie ist "unendlich genau"; geometrisch veranschaulicht stellt die Maßzahl des wahren Wertes einen Punkt auf der rellen Zahlenlinie dar.
Die wahre Maßzahl weist unendlich viele Nachkommastellen auf. Die Ziffernfolge dieser Zahl (die dem wahren Zahlenwert von \(m_e\) entspricht) hört nie auf.
Denken Sie bei reellen Zahlen beispielsweise an die Kreiszahl \(\pi\) oder die Eulersche Zahl \({\rm e}\), deren wahrer Wert durch keine noch so lange Ziffernfolge exakt angegeben werden kann. Wir kennen den wahren Wert der Zahl \(\pi\) überhaupt nicht, ganz gleichgültig, wie viele Stellen wir bereits ermittelt haben. Im Jahr 2019 waren 31 415 926 535 897 Stellen von \(\pi\) bekannt, das ist schon nicht schlecht, aber es ist natürlich auch nur ein Tropfen im Meer der Unendlichkeit.–
Hier finden Sie eine geradezu unglaubliche Eigenschaft von \(\pi\)
Wir kennen aber von keiner Größe die unendliche Ziffernfolge, die ihrer wahren Maßzahl entspricht. Im Laufe der Entwicklung stets verfeinerter Messmethoden wird die Folge zuverlässiger Ziffern immer länger, weil die Genauigkeit der Messungen immer weiter zunimmt. Das Intervall, innerhalb dessen der wahre Wert liegt, immer weiter einzuengen, ist ein historischer Prozess, ein Stück Wissenschafts- und Technikgeschichte.
Beispiel: Der aktuelle Wert der Rydberg-Konstante \(R_{\infty}\) beträgt nach dieser Quelle: \(R_{\infty} = 10 973 731,568 160\;{\rm m}^{-1} \). Das sind 14 Stellen; die letzten beiden Stellen sind unsicher. Die relative Unsicherheit beträgt nach derselben Quelle \(1,9 \cdot 10^{-12}\). Bei dieser Zahlenangabe handelt es sich um eine relative Standardunsicherheit
; wir werden später lernen, worum es sich dabei genau handelt. Im Jahr 2004 betrug die relative Unsicherheit noch \(7,6 \cdot 10^{-12}\), vor einigen Jahrzehnten war sie noch in der Größenordnung von \(10^{-9}\).
Die relative Unsicherheit gibt das Intervall an, innerhalb dessen wir die Maßzahl einer Größe kennen, bezogen auf den Wert der Größe.
Beispiel: Die aktuelle relative Unsicherheit der Rydberg-Konstanten beträgt: \(\delta R_{\infty} = 1,9 \cdot 10^{-12}\). Die absolute Intervallbreite \(\Delta R_{\infty}\) beträgt \[ \Delta R_{\infty} = R_{\infty} \cdot \delta R_{\infty} \approx 2\cdot 10^{-5}\;{\rm m}^{-1}. \]
Wir wollen nun etwas genauer herausarbeiten, inwieweit sich messtechnische Zahlen von den reellen Zahlen unterscheiden. Das hat mit den soeben genannten Intervallen zu tun.
Die reellen Zahlen bilden bekanntlich ein Kontinuum ohne Lücken. Wie gelangen wir, ausgehend von diesem Kontinuum, zu einer einzelnen, diskreten reellen Zahl?
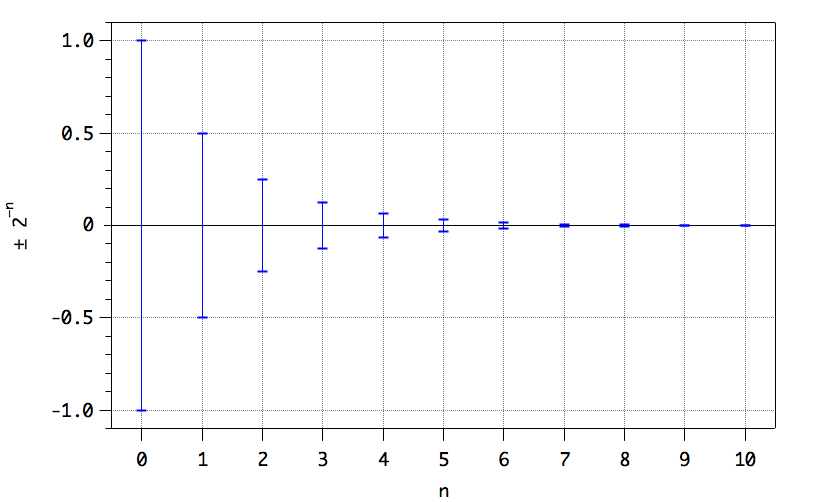
Wir betrachten die diskrete reelle Zahl (einen Punkt auf der Zahlengeraden) als Grenzwert eines immer kleiner werdenden Intervalls. Wir betrachten z.B. das Intervall von (-1) bis (+1) und halbieren es immer weiter:
\[ \left(-1,\;1\right),\left(-\frac{1}{2}, \frac{1}{2}\right),\; \left(-\frac{1}{4}, \frac{1}{4}\right),\;\left(-\frac{1}{8}, \frac{1}{8}\right),\;\left(\cdots\right) \] Die reelle Zahl Null können wir uns demnach vorstellen als den Grenzwert des Intervalls \(\left(-2^{-n},\;2^{-n}\right)\), wenn \(n\) gegen \(\infty\) geht: \[ 0 = \lim_{n \to \infty} \left(-2^{-n},\;2^{-n}\right). \]Eine reelle Zahl repräsentiert ein Intervall der Breite Null.
Beachten Sie, dass Sie durch beliebig häufiges Halbieren des Intervalls niemals zu der diskreten Zahl Null gelangen, sondern stets zu einem endlich breiten Intervall um Null herum, auch wenn es immer schmaler wird (vgl. Abb. 1-1).

Die Zahlen, die aus Messungen folgen, repräsentieren (fast) immer ein solches Intervall. Es kommt in der Messtechnik entscheidend darauf an, in Intervallen zu denken, und nicht in diskreten Zahlen.
Nehmen wir an, die Genauigkeit einer Messung (z.B. Messung der Planckschen Konstanten) würde sich alle zehn Jahre verdoppeln, die Breite des Intervalles, innerhalb dessen die Plancksche Konstante liegt, würde sich also alle zehn Jahre halbieren. Dann würden wir dennoch niemals (!) zum »wahren« Wert der Planckschen Konstanten gelangen (wenn es einen solchen denn gibt) - nach wie vielen Jahrzehnten sollte dies denn der Fall sein?
Eine Zahlenangabe, die aus einer Messung folgt, muss immer als Intervall erfolgen, außer, es handelt sich um eine Zählung.Bitte lesen Sie den folgenden Abschnitt aus dem Buch Was ist Mathematik von Richard Courant genau durch:

Das Zitat zeigt Ihnen, dass wir mit unserer Interpretation einer diskreten reellen Zahl als Grenzwert einer Intervallschachtelung und mit der messtechnischen Bedeutung der Intervalle in bester Gesellschaft sind.
Einen Sonderfall stellen Größen dar, die man zählen kann, wie die Zahl
der Eier in einem Karton (vgl. Nullter Übungsbogen). Bei diesen Größen ist die Maßzahl eine Ganzzahl.
Ganzzahlen sind als solche unendlich genau; sie repräsentieren für sich genommen keine Intervalle. Bei kleinen Ganzzahlen
macht es wenig Sinn, bei ihnen einen Fehler anzugeben:
»Die Zahl der Kohlenstoffatome in Benzol ist \(6\pm 0,1\)« ist Unsinn.
Wenn die Ganzzahlen aber größer werden, kann die Angabe eines Fehler durchaus sinnvoll sein,
z.B. bei der Anzahl Vögel in einem Schwarm von Wildgänsen. Das liegt daran, dass wir diese Anzahl normalerweise nicht durch Zählung, sondern durch Schätzung ermitteln.
Einen weiteren Sonderfall stellen Größen dar, die per definitionem auf einen bestimmten Wert festgelegt worden sind. Beispielsweise wurde der Wert der Lichtgeschwindigkeit auf exakt 299792458 m/s festgelegt.
Wir verstehen jetzt, warum die Annahme, es gebe einen wahren Wert einer Messgröße, eine experimentell unbewiesene Vermutung ist: wie klein auch immer das Ungenauigkeitsintervall sein mag, es bleibt doch immer ein endlich großes Intervall. Wir können also z.B. nicht experimentell beweisen, dass die Ruhemasse \(m_0\) aller Elektronen immer genau gleich groß ist: wir können ja nur das Intervall angeben, innerhalb dessen \(m_0\) liegt. Innerhalb dieses Intervalls könnte die Masse der Elektronen also unterschiedlich sein.
Auflösung.– Eine reelle Maßzahl \(\{M\}\) einer Messgröße \(M\) kann immer nur mit endlicher Genauigkeit registriert werden. In diesem Zusammenhang spielt ein sehr wichtiger Begriff zur Charakterisierung von Messgeräten (und damit von Messungen) eine Rolle: die Auflösung des Messgerätes.
Beispiel: Bei einem Spannungsmessgerät (Voltmeter), das mit einem Zeiger zur Anzeige der Spannung \(U\) ausgestattet ist, ist die Auflösung des Messbereiches diejenige Änderung \(\Delta U\) der zu messenden Spannung, die noch zu einer erkennbaren Änderung der Zeigerposition führt.
Wir unterscheiden die absolute Auflösung \(\Delta M\) und die relative Auflösung \(\delta M\) einer Messgröße \(M\).
Die absolute Auflösung \(\Delta M\) hat dieselbe Einheit wie die Messgröße. Ist beispielsweise die Messgröße die elektrische Spannung \(U\), so ist die Einheit der Größe und der Auflösung des Messgerätes: \([U] = [\Delta U] = {\rm V}\). Beispiel: der Messbereich eines Voltmeters beträgt 10 V, und die absolute Auflösung beträgt \(\Delta U = 10\;{\sf mV} = 10^{-2}\;{\rm V}\).
Die relative Auflösung \(\delta M\) ist gleich dem Quotienten aus dem Messbereich \(M\) und der absoluten Auflösung \(\Delta M\) in diesem Messbereich:
\begin{equation} \delta M = \frac{M}{\Delta M}. \end{equation}Beispiel: Für den Messbereich 10 V und eine absolute Auflösung von \(\Delta U = 10\;{\sf mV} \) beträgt die relative Auflösung: \[ \delta U = \frac{\rm 10\; V}{\rm 0,01\; V} = 1000. \]
Die relative Auflösung ist eine dimensionslose Größe und weist keine Einheit auf.
Die relative Auflösung darf nicht mit dem relativen Fehler verwechselt werden; der Bruch ist umgekehrt (siehe weiter unten). Leider wird für beides dieselbe Symbolik verwendet. Dass eine Größe und ihr Kehrwert mit demselben Symbol belegt werden, wird uns noch öfter begegnen. Rechnen Sie nicht damit, dass die technische Literatur in derselben Weise konsistent ist wie didaktisch aufbereitete Lehrbücher.
\paragraph {Angabe von Zahlen in den Naturwissenschaften:} Zahlen zur Angabe der Maßzahl von Messgrößen werden in den Naturwissenschaften typischerweise in Gleitkommazahl dargestellt. Am sinnvollsten erfolgt die Angabe einer Zahl (Z) als ($Z = {\rm Mantisse} \cdot 10^{\rm Exponent},)$ wie in folgendem Beispiel beschrieben: ($Z = 1,234 \cdot 10^{-4})$ Computerausgaben ersetzen das typographisch schwierig zu setzende \glqq mal zehn hoch\grqq~ durch ein \glqq E\grqq oder ein \glqq e\grqq, außerdem wird in US-amerikanischer Notation der Punkt als Dezimalseparator verwendet, also: ($Z = 1,234 \cdot 10^{-4} = 1.234{\rm E}23)$ Achtung: das e oder E trennt nur die Mantisse vom Exponent, es wird die Basis 10 (und nicht etwa die Eulersche Zahl (e)) verwendet. \paragraph{Normalisierte wissenschaftliche Zahlen.--} Wir stellen Zahlen unter Beachtung folgender Regeln dar: \begin{enumerate}[topsep=0pt,itemsep=-1ex,partopsep=1ex,parsep=1ex]Signifikante Stellen.– Jede messtechnische Zahl, die wir verwenden, repräsentiert ein Intervall; das Intervall entspricht normalerweise der Messungenauigkeit und ist durch die Auflösung des Messgerätes gegeben.
Die Zahlenangabe »1,7« bedeutet: 1,7 und nicht 1,6 oder 1,8. Die Zahl »1,7« steht also für das Intervall zwischen 1,65 und 1,75. Sie repräsentiert dieses Intervall. (Für unsere Zwecke ist es irrelevant, ob die Grenzen gerade noch zum Intervall gehören oder nicht.)
Sie können es sich vorstellen wie die Bretter eines Zaunes:
Es kommt also darauf an, die Intervallbreite bei einer Zahlenangabe so einzustellen, dass sie einer Messgenauigkeit entspricht. Dies realisiert man durch das Konzept der signifikanten Stellen einer Maßzahl.
Wichtige Regeln für die sogenannte normalisierte wissenschaftliche Notation einer Zahl, die wir im Folgenden nutzen wollen:
\(N_{A} =\) 6,022 \(\cdot 10\)\(^{23}\).
Die Mantisse ist also gleich 6,022 und der Exponent ist gleich 23.
Wenn nachfolgend von wissenschaftlicher Notation die Rede ist, so ist stets die normalisierte Notation darunter zu verstehen.
Neben der normalisierten wissenschaftlichen Notation gibt es noch die sogenannte technische Notation (englisch engineering notation). In dieser Notation wird die Mantisse so geschrieben, dass der Exponent ein Vielfaches von Drei ist. Dies hat den Vorteil, dass der Exponent unmittelbar in einen Einheitenvorsatz wie »milli« oder »nano« umgerechnet werden kann. Mehrere Ziffern vor dem Komma sind erlaubt, eine Null vor dem Komma ist erlaubt. Beispiele für die technische Notation und ihre Umrechnung in normalisierte wissenschaftliche Notation:
Rechnen mit signifikanten Stellen.– Für das Rechnen mit signifikanten Stellen gelten spezielle Regeln.