\(\newcommand{\diff}{{\rm d}}\) \(\newcommand{\pdiff}{{\partial}}\)

Lösungen zum fünften Übungsbogen

Q4-0 — Elektrischer Widerstand

Welche der nachfolgend genannten Aussagen treffen zu?

   Welche der folgenden Aussagen treffen zu:    (A)      Nahezu jedes materielle Medium setzt dem elektrischen Stromfluss einen Widerstand entgegen, der den Stromfluss hemmt.

(B)      In einem materiellen Medium erfolgt ein dauernder Stromfluss nur unter dem Einfluss einer andauernden Potentialdifferenz längs des Mediums.

(C)      Das elektrische Potential und die elektrische Spannung weisen voneinander verschiedene Einheiten auf.

(D)      Wenn der Widerstand eines Materials doppelt so groß ist wie der eines anderen, so benötigt man eine doppelt so hohe Potentialdifferenz, um den gleichen Strom darin fließen zu lassen.

Lösung:

(A), (B) und (D) sind richtig; dies ergibt sich alles aus der 6. Vorlesung. (C) ist verkehrt, den die elektrische Spannung ist nichts weiter als eine elektrische Potentialdifferenz, folglich hat sie dieselbe Einheit wie das elektrische Potential.

Q4-1 — Elektrische Leistung

Eine Glühlampe hat eine Leistungsaufnahme von \(P = 60\;{\rm W}\) und eine Betriebsspannung von \(U = 240\;{\rm V}\). Welchen elektrischen Widerstand weist die Glühlampe im laufenden Betrieb auf?

(A)       \( 3,456\cdot 10^6\;\Omega\)

(B)      \( 960\;\Omega\)

(C)      \(4 \;\Omega\)

(D)      Aus den genannten Daten lässt sich das Ergebnis nicht ermitteln.

Lösung:

Wir betrachten die Gl. (7) der 6. Vorlesung: \begin{equation*} P = U \cdot I = \frac {U^2}{R} = I^2 \cdot R. \end{equation*} Durch Umstellen erhält man sofort: \begin{equation*} R = \frac {U^2}{P} = \frac{240^2\;{\rm V^2}}{60\;{\rm V \cdot A}} = 960\;\Omega. \end{equation*}

Q4-2 Belastbarkeit von Widerständen—

Ein Widerstand \(R= 5,0\cdot10^{1}\;\Omega\) ist mit einer elektrischen Leistung von \(P=0,25\;{\rm W}\) belastbar. Welche maximale Spannung \(U_{\rm max}\) darf an dem Widerstand abfallen?

   Die maximale Spannung \(U_{\rm max}\) beträgt:    (A)      \(13\;{\rm V}\)
(B)      \(1,5\;{\rm V}\)
(C)      \(3,5\;{\rm V}\)
(D)      \(130\;{\rm V}\)

Lösung:

Mit \[ P = U \cdot I \] und \[ I = \frac{U}{R} \] folgt \[ P=\frac{U^{2}}{R}, \] also \[ P \cdot R = U^{2}, \] daher auch \[ P_{\rm max} \cdot R = U^{2}_{\rm max} \] und \[ \sqrt{P_{\rm max}\cdot R} = U_{\rm max}, \] also \[ U_{\rm max} = \sqrt{\rm 0,25\;W \cdot 50\;\Omega} = 3,5\;{\rm V}. \] An dem Widerstand dürfen nicht mehr als \(U_{\rm max} = 3,5\;{\rm V}\) abfallen ( = anliegen).

Q4-3 —Ohmsches Quadrat

Das Ohmsche Quadrat ist eine vereinfachte Version des Ohmschen Würfels für Nebenfächler. Es ist in der folgenden Abbildung dargestellt.

Das Ohmsche Quadrat.

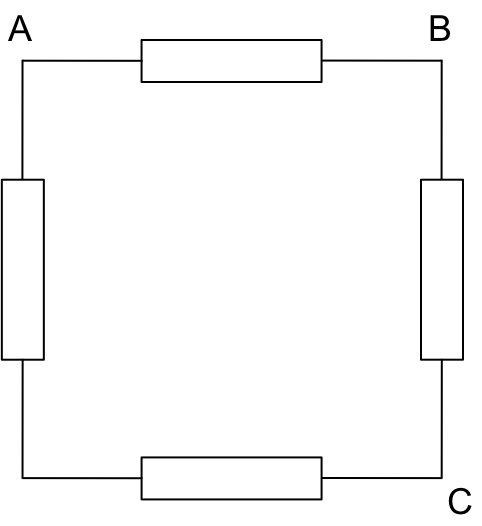
Alle vier Widerstände haben einen Wert von jeweils \(R=100\;\Omega\). Berechnen Sie den Widerstand zwischen den Punkten A und B!

    Der Widerstand zwischen den Punkten A und B beträgt:    

(A)       \(75\;\Omega\)

(B)       \(400\;\Omega\)

(C)       \(200\;\Omega\)

(D)       Die anderen drei Antworten sind falsch.

Lösung:

Zwischen den Punkten A und B sind einander parallel geschaltet:

  1. Drei in Serie geschaltete Widerstände zu je \(100\;\Omega\); diese ergeben einen Gesamtwiderstand von \(300\;\Omega\).
  2. Ein Widerstand zu \(100\;\Omega\).
  3. Für den Kehrwert des Gesamtwiderstandes der parallel geschalteten Widerstände von \(300\;\Omega\) und \(100\;\Omega\) gilt: \[ \frac{1}{R} = \frac{1}{300\;\Omega} + \frac{1}{100\;\Omega} = \frac{4}{300\;\Omega} \] Damit ist \[ R = \frac{300\;\Omega}{4} = 75 \Omega.\]

Die Anordnung weist zwischen den Punkte A und C einen Widerstand von \(100\;\Omega\) auf.

Eine solche Schaltung baut man auf, weil die Widerstände eine vierfach höhere Leistung vertragen als ein einzelner Widerstand von \(100\;\Omega\).

Q4-4 —Ohmsches Quadrat (zweiter Teil)

Das Ohmsche Quadrat ist eine vereinfachte Version des Ohmschen Würfels für Nebenfächler. Es ist in der folgenden Abbildung dargestellt.

Das Ohmsche Quadrat.

Alle vier Widerstände haben einen Wert von jeweils \(R=100\;\Omega\). Berechnen Sie den Widerstand zwischen den Punkten A und C!

    Der Widerstand zwischen den Punkten A und C beträgt:    

(A)       \(75\;\Omega\)

(B)       \(200\;\Omega\)

(C)       \(100\;\Omega\)

(D)       Die anderen drei Antworten sind falsch.

Lösung:

Zwischen den Punkten A und C sind einander jeweils zwei in Serie geschaltete Widerstände parallel geschaltet.

  1. Zwei in Serie geschaltete Widerstände zu je \(100\;\Omega\) ergeben einen Gesamtwiderstand von \(200\;\Omega\).
  2. Für den Kehrwert des Gesamtwiderstandes der parallel geschalteten Widerstände von je \(200\;\Omega\) gilt: \[ \frac{1}{R} = \frac{1}{200\;\Omega} + \frac{1}{200\;\Omega} = \frac{2}{200\;\Omega} = \frac{1}{100\;\Omega} \] Damit ist \[ R = 100\;\Omega.\]

Die Anordnung weist zwischen den Punkte A und C einen Widerstand von \(100\;\Omega\) auf.

Eine solche Schaltung baut man auf, weil die Widerstände zusammen eine vierfach höhere Leistung vertragen als ein einzelner Widerstand von \(100\;\Omega\).

Q4-5 —Stromfluss durch Widerstände

Betrachten Sie die folgende Schaltung aus drei parallel geschalteten Widerständen (\(100\;\Omega,\;200\;\Omega,\;300\;\Omega\)), die gemeinsam an eine Spannungsquelle \(U=5\;{\rm V}\) angeschlossen sind.

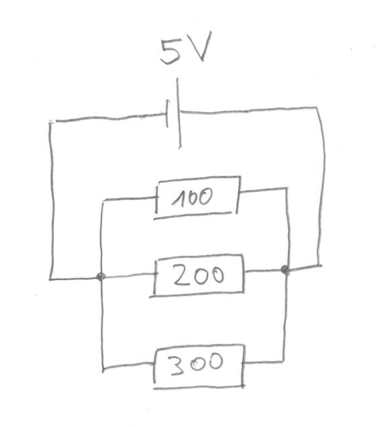
Drei parallel geschaltete Widerstände.

Welcher Anteil des fließenden Stromes in Prozent fließt durch den Widerstand \(R=300\;\Omega\)?

   Der Anteil des fließenden Stromes in Prozent beträgt ungefähr:     (A)      \(50\%\)
(B)      \(33\%\)
(C)      \(18\%\)
(D)      Die anderen drei Antworten sind nicht einmal anähernd richtig.

Lösung:

(C) ist richtig.

Bezeichnen wir \(R_1 = 100\;\Omega\) einfach mit \(R\), dann ist \(R_2=2R\) und \(R_3=3R\).
Der fließende Gesamtstrom ist:
\(I_{\sum} = I_1 + I_2 + I_3 = \frac{U}{R} + \frac{U}{2R} + \frac{U}{3R}\). Das Verhältnis \(\frac{I_3}{I_{\sum}}\) ist dann gleich \[ \frac{I_3}{I_{\sum}} = \frac{U}{3R \cdot \left( \frac{U}{R} + \frac{U}{2R} + \frac{U}{3R}\right)} = \frac{U}{3U + \frac{3}{2}U + U} = \frac{U}{5\frac{1}{2}\; U} = \frac{1}{5\frac{1}{2}} = \frac{2}{11} \approx 18\%.\]

Q4-6 —Spannungsteiler

Betrachten Sie die folgende Schaltung:

Schaltung zu Aufgabe Q4-6.

Welche Spannung \(U_1\) fällt an dem Widerstand \(R=150\;\Omega\) ab?

   \(P = \)    (A)      \(6,0\;{\rm V}\)

(B)      \(2,4\;{\rm V}\)

(C)      \(3,6\;{\rm V}\)

(D)      Keine der Antworten ist auch nur annähernd richtig.

Lösung:

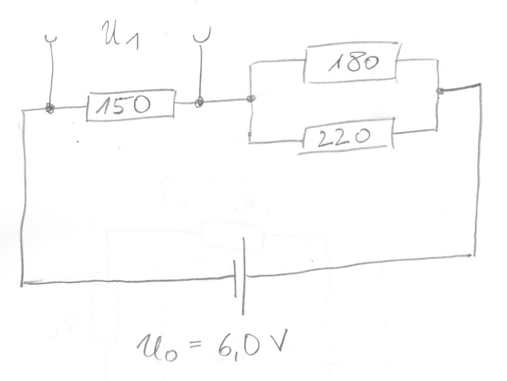
Die beiden parallel geschalteten Widerstände zu \(180\;\Omega\) und \(220\;\Omega\) sind in Serie mit dem \(150\;\Omega\)-Widerstand geschaltet.

Der Kehrwert des Gesamtwiderstandes der parallel geschalteten Widerstände beträgt: \[ \frac{1}{R} = \frac{1}{180\;\Omega} + \frac{1}{220\;\Omega} = 0,010101\dots \Omega^{-1} \] Der Widerstand beträgt \[ \Omega = 99\;\Omega. \]

Es sind also Widerstände von \(150\;\Omega\) und \(99\;\Omega\) in Serie geschaltet. Die am \(150\;\Omega\)-Widerstand abfallende Spannung \(U_1\) berechnet sich nach Gl. (12) der 6. Vorlesung zu \[ U_1 = U_0 \cdot \frac{R_1}{R_1+R_2} = 6,0\;{\rm V} \cdot \frac{150}{150 + 99} = 6,0\;{\rm V} \cdot 0,60 = 3,6\;{\rm V} \]

Q4-7 —Spannungsabfall am Innenwiderstand

Die Batterie eines Radios hat die Klemmspannung \(U=9,00\;{\rm V}\). Bei einer Stromentnahme von \(20,0\;{\rm mA}\) ist die Klemmspannung auf \(8,80\;{\rm V}\) abgesunken. Welchen inneren Widerstand hat die Batterie?

   Der Innenwiderstand der Batterie beträgt:    (A)      \(10,0\;\Omega\).

(B)      \(1,00\;\Omega\)

(C)      \(100\;\Omega\)

(D)      Keine der Antworten ist auch nur annähernd richtig.

Lösung:

(A) ist richtig.

\begin{align*} U_{Kl} &= U_0 - R_i \cdot I; \\ 8,80\;{\rm V} &= 9,00\;{\rm V} - R_i \cdot 20,0\;{\rm mA}; \\ 9,00\;{\rm V} - 8,80\;{\rm V} &= R_i \cdot 20,0\;{\rm mA}\\ \frac{9,00\;{\rm V} - 8,80\;{\rm V}}{ 20,0 \;{\rm mA}} &= R_i \\ \frac{200\;{\rm mV} }{ 20,0 \;{\rm mA}} &= R_i \\ R_i &= 10,0\;\Omega. \end{align*} Die Batterie weist einen Innenwiderstand von \(R_i = 10,0\;\Omega\) auf.

Q4-8 —Elektrische Netzwerke

Hier ist eine Aufgabe aus einer Vorlesung für Elektrotechniker an der TU, Elektrische Netzwerke. Zeigen Sie mal, dass Sie das können. Los, machen Sie schon.

Ein Widerstandsnetzwerk.

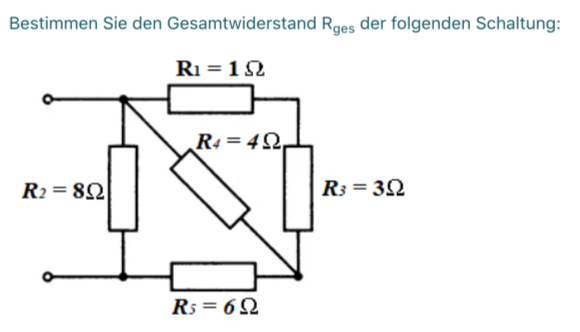
Unter Gesamtwiderstand ist der Widerstand zu verstehen, den man an den beiden Anschlussklemmen an \(R_2\) misst. Wenn Sie die Aufgabe knacken wollen, müssen Sie lernen, es richtig zu sehen. Was ist dem Widerstand \(R_2=8\;\Omega\), über den der Gesamtwiderstand gemessen wird, parallel geschaltet? Die Aufgabe ist so ähnlich wie Q4-3, aber zusätzlich gibt es hier noch den Widerstand \(R_4\). \(R_4\) ist \(R_1 + R_3\) parallel geschaltet, und der aus \(R_4\) und \(R_1 + R_3\)resultierende Widerstand ist in Serie mit \(R_5\) geschaltet. Na? Kommen Sie drauf? 😁

   Der Gesamtwiderstand beträgt:     (A)      \(2\;\Omega\)

(B)      \(4\;\Omega\)

(C)      \(8\;\Omega\)

(D)      Keine der anderen Antworten ist auch nur annähernd richtig.

Lösung:

(B) ist richtig.

Dem Widerstand \(R_2\) ist parallelgeschaltet ein Widerstand \(R_5 = 6\;\Omega\); dieser ist in Serie geschaltet mit einem Widerstand, der sich aus \(R_1\), \(R_3\) und \(R_4\) zusammensetzt. \(R_3\) und \(R_1\) sind in Serie geschaltet, ihr Gesamtwiderstand ist gleich \(4\;\Omega\). Diesen \(4\;\Omega\) ist \(R_4=4\;\Omega\) parallel geschaltet. Zwei einander gleiche parallel geschaltete Widerstände haben zusammen den halben Widerstand, also \(2\;\Omega\). Also sind \(6\;\Omega\) (von \(R_5\) und \(2\;\Omega\) in Serie geschaltet, das ergibt zusammen \(8\;\Omega\).

Insgesamt ist dem Widerstand \(R_2=8\;\Omega\) also ein Widerstand von \(8\;\Omega\) parallel geschaltet. Damit beträgt der Gesamtwiderstand \(4\;\Omega\).

Q4-9 —Kurzschlussstrom

Nehmen wir an, eine Spannungsquelle weise eine Ruhespannung (Leerlaufspannung, Spannung bei \(I=0\) von \(U_0=1,23\;{\rm V}\) auf. Der Innenwiderstand der Quelle sei zu \(R_i=16,5\;\Omega\) gegeben. Wie groß ist der Kurzschlussstrom der Quelle, der sich einstellt, wenn man die Pole der Quelle mit einem Draht verbindet?

   Der Kurzschlussstrom beträgt in der Einheit \({\rm mA}\):    












Lösung: Antwort (A) ist richtig.
Wenn die Quelle kurzgeschlossen ist, dann ist nur der Innenwiderstand der Quelle strombegrenzend. Ein äußerer Lastwiderstand liegt ja nach Voraussetzung nicht an; statt dessen ist die Quelle mit einem Draht vernachlässigbaren Widerstandes kurzgeschlossen.
Also gilt für die kurzgeschlossene Quelle: \begin{equation*} \frac{U_0}{R_i} = I = \frac{\rm 1.23\;V}{16.5 \; \Omega} = 0,0745\;{\rm A} = 74.5\;{\rm mA}. \end{equation*}

Q4-10—Experimentelle Bestimmung des Innenwiderstandes einer Spannungsquelle

Eine elektrochemische Spannungsquelle wird experimentell charakterisiert, indem die Klemmspannung \(U_{kl}\) für unterschiedliche Lastwiderstände gemessen wird. Dabei ergeben sich folgende Wertepaare:

\(\frac{R_a}{\rm \Omega}\)\(\frac{U_{kl}}{\rm V}\)
0.50.24
10.39
20.58
40.76
50.81
100.93
150.98
201.01
351.05
501.06
Bestimmen Sie mit diesen Angaben den Innenwiderstand \(R_i\) der Spannungsquelle!

   \(R_i = \)   













Lösung:

(B) ist richtig.

Übergabe der Werte nach Igor und Berechnung des fließenden Stromes ergibt folgende Tabelle (die Werte für den Strom ergeben sich aus den Elementen von rw! und uW1 durch Division):

Abb. Q4-10-1: Nach Igor übertragene Werte und entsprechende Stromflüsse.

Die graphische Darstellung und die lineare Regression ergeben:

Abb. Q4-10-2: Graphische Darstellung der Werte und lineare Regression.

In der Abbildung ist der Innenwiderstand (mit falschem Vorzeichen) bereits eingetragen.

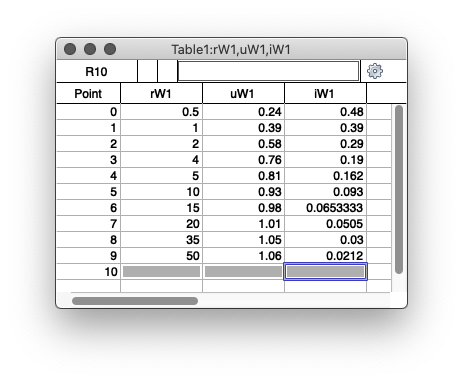
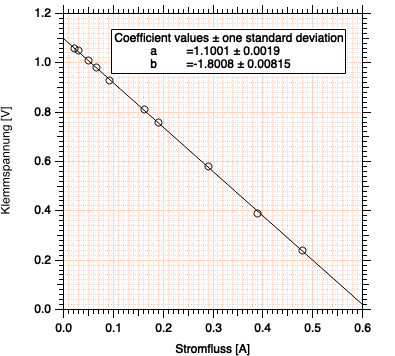
Q4-11— Experimentelle Bestimmung der Leerlaufspannung einer Spannungsquelle

Diese Aufgabe ist die Fortsetzung der Aufgabe Q4-10; es werden dieselben Daten verwendet. Bestimmen Sie mit den Werten aus der Tabelle in Aufgabe Q4-10 die Leerlaufspannung \(U_0\) der Spannungsquelle!

   \(U_0 = \)   













Lösung:

(D) ist richtig.

Dies ergibt sich aus der Lösung der Aufgabe Q4-10, die Leerlaufspannung ist in die Abbildung eingetragen.

Q4-12— Experimentelle Bestimmung des Kurzschlussstroms einer Spannungsquelle

Diese Aufgabe ist die Fortsetzung der Aufgabe Q4-10 und Q4-12; es werden dieselben Daten verwendet. Bestimmen Sie mit den Werten aus der Tabelle in Aufgabe Q4-10 den Kurzschlussstrom \(I_k\) der Spannungsquelle!

   \(I_k = \)   













Lösung:

(A) ist richtig.

Dies ergibt sich aus der Lösung der Aufgabe Q4-10, die Leerlaufspannung ist in die Abbildung eingetragen.

Zur Bestimmung des Kurzschlussstromes brauchen wir lediglich die Leerlaufspannung durch den Innenwiderstand zu teilen (vgl. 6. Vorlesung): \[ I_{k} = \frac{U_0}{R_i} = 0.6108\;{\rm A} \] Außerdem ist \[\delta I_k = \sqrt{\delta U_{0}^2 + \delta R_{i}^2} = \sqrt{\left(\frac{0.002}{1.1}\right)^2 + \left(\frac{0,008}{1.801}\right)^2} \approx 4.8 \cdot 10^{-3} \] \[\Delta I_k = \delta I_k \cdot I_k = 0.6108\;{\rm A} \cdot 4.8\cdot 10^{-3} \approx 0.003 \; {\rm A} \] \[ I_k = \left(0.611 \pm 0.003 \right)\;{\rm A}. \]

Q4-13 — Heizleistung

Betrachten Sie das Bild in dieser Abbildung. Es handelt sich um die Typenbeschriftung eines Heißluft-Handtrockners. Bei einer Netzspannung von \(U=220\;{\rm V}\) beträgt die Leistung des Heizelementes: \(W=2000\;{\rm W}\). Um wieviel Prozent steigt die Heizleistung an, wenn die Netzspannung \(U=240\;{\rm V}\) beträgt? Der Heizwiderstand ist als konstant zu betrachten.

   Die Heizleistung steigt um etwa:    



Lösung:

(A) ist richtig.

Da \(p=\frac{U^2}{R}\) und der Heizwiderstand als konstant betrachtet wird, gilt \[ \frac{U_2^2}{U_1^2} = \frac{P_2}{P_1} = 1.19, \] also steigt die Heizleistung um 19%.

Q4-14 — Überlandleitung (1)

Ein Kraftwerk versorgt eine Ortschaft mit Elektrizität. Die Leitung zur Siedlung und zurück beträgt insgesamt 24 km. Der Innenwiderstand des verwendeten Drahtes beträgt \(\frac{0.2\;\Omega}{\rm km}\). Wir betrachten die gesamte Siedlung als einen Verbraucher mit einem Stromverbrauch von 1000 A bei einer Sollspannung von \(U = 220\;{\rm V}\).
Wieviel Prozent der vom Kraftwerk produzierten Leistung \(P_{\Sigma}\) werden durch die Verbraucher in der Siedlung genutzt (drei signifikante Stellen)?

   Von den Verbrauchern werden genutzt:   




Antwort (C) ist richtig. \[ U = U_0 - I \cdot R \to U_0 = U + I\cdot R_I = 220\;{\rm V} + 1000\;{\rm A} \cdot \frac{0,2\;\Omega}{\rm km} \cdot 24\;{\rm km} \] \[= (220 + 4800)\;{\rm V} = 5020\;{\rm V}.\] \[P_{\Sigma} = U \cdot I = 5020 \; {\rm V} \cdot 1000\;{\rm A} = 5.02\cdot 10^{6} \; {\rm W}.\] \[P_V = 220\;{\rm V} \cdot 1000 \; {\rm A} = 2.20 \cdot 10^5 \; {\rm W} \] \[\frac{2.20 \cdot 10^5 \; {\rm W} }{5.02\cdot 10^{6} \; {\rm W}} \approx 4.38\%.\] Die Ausbeute beträgt unter den genannten Bedingungen 4.38 %. 95.62% der produzierten Leistung werden in der Freileitung in Wärme umgesetzt, also nahezu alles.

Q5–15 — Überlandleitung (2)

Das Kraftwerk aus Aufgabe 5-14 wird umgerüstet: die an die Leitungen angelegte Spannung wird auf \(U_0=380\;{\rm kV}\) erhöht. Die Hochspannung wird erst vor Ort durch einen Transformator (Stromhäuschen) auf 220  herabgesetzt. Die Leitung zur Siedlung und zurück beträgt insgesamt 24 km. Der Innenwiderstand des verwendeten Drahtes beträgt \(\frac{0.2\;\Omega}{\rm km}\). Wir betrachten die gesamte Siedlung als einen Verbraucher mit einem Stromverbrauch von 1000 A bei einer Sollspannung von \(U = 220\;{\rm V}\).
Wieviel Prozent der vom Kraftwerk produzierten Leistung \(P_{\Sigma}\) werden unter den geänderten Bedingungen in der Freilandleitung in Wärme umgewandelt, also nicht durch die Verbraucher genutzt?

   In der Freilandleitung werden umgesetzt:   



Antwort (D) ist richtig. \[P_V = 220\;{\rm V} \cdot 1000\;{\rm A} = 2.20 \cdot 10^5 \; {\rm W}. \] \[ 220\;{\rm V} \cdot 1000 \; {\rm A} = 380\cdot 10^3 \;{\rm V} \cdot 0.579\; {\rm A}. \] Durch die Freileitung fließen 0.579 A.
Spannungsverlust \(U_L\) in der Leitung:
\[ U_L = R_i \cdot I = \frac{0.2\;\Omega}{\rm km} \cdot 24\;{\rm km} \cdot 0.579\;{\rm A} = 2.78\;{\rm V}. \] Leistungsverlust in der Leitung: \[ 3.80\cdot 10^3\;{\rm V} \cdot 0.579\;{\rm A} = 2.20\cdot 10^5\; {\rm W} \] \[ \frac{1.61\; {\rm W}}{2.20\cdot 10^5\; {\rm W}} = 7.32\cdot 10^{-4}\;\%. \] Der Leistungsverlust in der Leitung beträgt ca. 0.0007 %, ist also vollkommen vernachlässigbar.