Es handelt sich offenbar um einen großen Datensatz. Die Daten stellen eine Liste dar, deren Eintrage jeweils durch ein Zeilenende-Zeichen voneinander separiert sind. (Es gibt auch sogenannte CSV-Dateien (
comma separated values)).
Das Ausrechnen mit dem Taschenrechner ist quälend und kann schnell zu Fehlern beim Abtippen führen. Hierfür ist ein Computer sehr viel besser geeignet. Wir verwenden zur Datenanlyse IGOR PRO, aber die Aufgabe lässt sich ebenso gut mit einem anderen geeigneten Computerprogramm lösen (Excel zum Beispiel).
edit
eingeben.Wir klicken auf das erste Element der ersten Spalte und kopieren (»pasten«) den Inhalt der Zwischenablage in diese Spalte. Es wird dann automatisch von Igor aus den Daten eine wave mit dem Namen wave0 erzeugt.
Den Mittelwert können wir uns entweder ausgeben lassen durch Eingabe des Befehls
Q3-2 —Probenstandardabweichung \(\sigma_P\)
Berechnen Sie die Probenstandardabweichung \(\sigma_P\) der Ihnen bereits aus Frage Q3-1 bekannten Gewichts-Liste (Link) mit zwei signifikanten Stellen!
Lösung:
(B) ist richtig. Berechnen Sie den Fehler des Mittelwertes \(\Delta \mu\) der Ihnen bereits aus den Aufgaben Q3-1 und Q3-2 bekannten Liste mit Gewichtsdaten (Link) in der Einheit \({\rm kg} \) mit zwei signifikanten Stellen!
Lösung:
(D) ist richtig. Wenn die Werte bereits in Igor eingelesen worden sind (und dort z.B. als wave0 existieren), dann liefert der Befehl wavestats wave0 eine Liste statistisch relevanter Daten, unter anderem auch den mittleren Fehler des Mittelwertes, der in der Ausgabe als V_sem bezeichnet wird (sem=standard error of the mean). Wir brauchen eigentlich nur den Zahlenwert abzulesen.
Gegeben seien Ihnen die folgenden fehlerbehafteten Ergebnisse (die Einheiten sind hier irrelevant): \(x_1 = 2,3 \pm 0,15\)
Lösung:
(C) ist richtig. Wir müssen die Gleichungen (6) und (7) aus der vierten Vorlesung anwenden. Wir erzeugen in einem beliebigen Tabellenkalkulationsprogramm die folgenden Spalten:
In die ersten beiden Spalten tragen wir die uns gegebenen Werte ein, die anderen Spalten lassen wir berechnen. Hier wurde dies beispielhaft für \(x=2,3 \pm 0,15\) gezeigt. Die Zeile mit den Symbolen \(x\), \(\Delta x\) u.s.w. ist (jedenfalls in Excel) die Zeile 1. Das erste Element dieser Zeile hat die Nummer A1, das zweite Element die Nummer B1, und so weiter. Das Quadrat des Fehlers von \(x_1\), also \(\Delta x_1\), erhalten wir durch Klicken in die dafür vorgesehene Zelle C2 und Eingeben des Befehls: =B2^2
Nachdem die Liste in der vorherigen Aufgabe bereits in Igor importiert wurde, können wir den Befehl
Q3-3 —Fehler des Mittelwerts
Q3-4 —Mittelwert fehlerbehafteter Größen
\(x_2 = 2,1 \pm 0,3\)
\(x_3 = 2,4 \pm 0,1\)
A B C D E 1 \(x\) \(\Delta x\) \((\Delta x)^2\) \(\frac{1}{(\Delta x)^2}\) \(\frac{x}{(\Delta x)^2} \) 2 \(2,3\) \(0,15\) \(0,0225\) \(44,444\) \(102,222 \)
=1/C2
Klicken in E2 und Eingeben der Formel
=A2/C2
liefert \(\frac{x}{(\Delta x)^2} \).Wenn wir die Ergebniszelle anklicken, in die Zwischenablage kopieren und in die entsprechenden Zellen der nächsten Zeilen einfügen, aktualisiert Excel automatisch die Indizes in der Formel und liefert die gewünschten Werte für die jeweiligen Startzahlen von \(x\) und \(\Delta x\).
Jetzt muss als Nächstes die Summer unter den Spalten D und auch E gebildet werden; dies kann man in Excel graphisch machen (es gibt einen \(\sum\) Button, oder wir schreiben von Hand in das Element D5:
=SUMME(D2:D4)
und entsprechend für E.
Teilen dieser Summen durcheinander liefert den gewichteten Mittelwert von \(\mu =2,35\) (auf drei signifikante Stellen gerundet).
Den Fehler des Mittelwertes erhalten Sie durch den Befehl
=WURZEL(1/SUMME(D2:D4))
Dies liefert für den Fehler den Wert \( \Delta \mu = 0,0802 \).
Beachten Sie bitte, dass der Fehler des Mittelwertes kleiner ist als die Fehler der Einzelwerte!
Q3-5 —Gewichteter Mittelwert
Welche der folgenden Aussagen treffen zu (Mehrfachauswahl)?
Lösung:
(B) und (D) sind richtig. (A) ist verkehrt, wie die Gleichungen (6) und (7) der Vorlesung zeigen. (B) ist richtig, die Wichtungsfaktoren ergeben sich aus den jeweiligen individuellen Fehlern. (C) ist falsch, und ist einer der am meisten gemachten Fehler im Praktikum! Die Leute bilden einfach den Mittelwert der individuellen Fehler. Das stimmt aber überhaupt nicht. (D) ist richtig; in Aufgabe 45 wurde dies an einem Beispiel gezeigt. Durch Verwendung hinreichend großer Datensätze kann der Fehler des gewichteten Mittelwertes sehr klein werden. Die Zuverlässigkeit des Mittelwertes kommt also aus der statistischen Analyse der Gesamtheit der Daten und nicht unmittelbar aus der Zuverlässigkeit der Einzelwerte.
Q3-6 — Statistische Auswertung eines Datensatzes
Die nachfolgende Liste zeigt die Ergebnisse der Teilnehmer an der ersten Übung in erreichten Punkten:
Berechnen Sie den Mittelwert \(\mu\) des Ergebnisses sowie die Standardabweichung \(\sigma_{P}\) in Prozent mit jeweils zwei signifikanten Stellen, wenn insgesamt 12 Punkte zu erreichen waren. Die Funktion wavestats des Programmes Igor Pro ist hier sehr hilfreich.
(A) ist richtig.
Der Datensatz muss an ein Programm übergeben werden, das statistische Auswertungen beherrscht; wir zeigen hier die Vorgehensweise, wenn Igor Pro verwendet wird.
Zum Import obiger Liste in Igor muss zunächst das Semikolon als Trennzeichen durch ein Komma ersetzt werden. Dies kann mit einem beliebigen Texteditor gemacht werden. Alle gängigen Betriebssysteme weisen einen eingebauten Texteditor auf; ich empfehle Nutzern eines Windows-Betriebssystems aber die Installation des Editors Notepad++ und Mac-Nutzern bbedit. Beide Programme sind kostenlos (bbedit hat eine kostenpflichtige Version, die Sie aber nicht brauchen werden, es sei denn, Sie verbringen Ihr Leben vor einem Editor).
Der Befehl zum Import der für Igor aufbereitete Liste lautet:
make testWave ={10, 10, 8, 4, 11, 10, 4, 10, 10, 7, 10, 7, 10, 6, 11, 7, 10, 12, 12, 12, 12, 12, 2, 10, 7, 5, 12, 12, 9, 9, 6, 8, 8, 12, 7, 10, 12, 3, 12, 11, 12, 10, 11, 12, 9, 10, 7, 8, 9, 9, 8, 12, 8, 8, 11, 8, 10, 7, 12, 7, 8, 12, 11, 6}Diesen Befehl können Sie unmittelbar in die Igor-Kommandozeile kopieren. Der Name testWave für die Wave ist natürlich völlig beliebig.
Danach müssen Sie lediglich den Befehl wavestats auf die Wave testWave anzuwenden:
wavestats testWave
Der Mittelwert \(\mu\) ist in der Variablen V_avg enthalten; es ist hier V_avg=9.14062.
Die Standardabweichung \(\sigma_P\) ist in der Variablen V_sdev enthalten; Igor liefert: V_sdev = 2.48722.
Die gesuchten Ergebnisse in Prozent erhalten Sie durch:
print V_avg/12*100
print V_sdev/12*100
Sie erhalten dann in der Igor-History die folgende Ausgabe:

Q3-7 —Gausssche Verteilungsfunktion
Welche der nachfolgend genannten Aussagen zur Gaussschen Verteilngsfunktion \(g(x)\) treffen zu?
(C) und (D) treffen zu.
(A) ist falsch, weil die Gauss-Funktion auf Eins normiert sein muss.
(B) ist falsch, weil \(g(x)\) nicht eine Wahrscheinlichkeit angibt, sondern eine Wahrscheinlichkeitsdichte. (C) ist richtig, ein Flächenabschnitt unter der Kurve gibt die Wahrscheinlich an, ein Ereignis in diesem Intervall anzutreffen. (D) ist richtig; \(g(x)\) wird zwar für \(x\)-Werte fern von \(\mu\) sehr klein, aber niemals streng gleich Null. Die Zahlenwerte \(x=\pm \infty\) gelten nicht, denn das sind keine rellen Zahlen.
Q3-8 — Gausssche Verteilungsfunktion
Gegeben sei Ihnen eine Gausssche Verteilungsfunktion mit den folgenden Parametern:
\(\mu = 7,23; \sigma = 1,35\).
Berechnen Sie den Wert der Gauss-Funktion an der Stelle \(x=6,00\) mit drei signifikanten Stellen!
Lösung:
Antwort (C) trifft zu. Man muss die Gauss-Funktion aufstellen und die Parameter \(\mu\) und \(\sigma\) einsetzen. Die Gauss-Funktion lautet (5. VL, Gl. 3):
\begin{equation*}
g(x) = \frac{1}{\sigma}
\cdot \sqrt{\frac{1}{2 \pi}}
\cdot \exp \left(
- \frac{1}{2} \frac{\left(x - \mu \right)^{2} }{\sigma^{2}} \right)
\end{equation*}
... und nach Einsetzen:
\begin{equation*}
g(x) = \frac{1}{1,35}
\cdot \sqrt{\frac{1}{2 \pi}}
\cdot \exp \left(
- \frac{1}{2} \frac{\left(x - 7,23 \right)^{2} }{1,35^{2}} \right)
\end{equation*}
Jetzt muss man den Wert für \(x\), also \(x=6\), einsetzen:
\begin{equation*}
g(x) = \frac{1}{1,35}
\cdot \sqrt{\frac{1}{2 \pi}}
\cdot \exp \left(
- \frac{1}{2} \frac{\left(6 - 7,23 \right)^{2} }{1,35^{2}} \right)
\end{equation*}
Die Gleichung enthält jetzt nur noch Zahlen, so dass man das Resultat ausrechnen kann. Viel einfacher geht das alles mit Igor:
Auf drei signifikante Stellen gerundet ergibt sich:
\[ g(6) = 0,195. \]
Q3-9 Gauss-Funktion und Wahrscheinlichkeit—
Wie groß ist die Wahrscheinlichkeit \(P\) mit drei Stellen, ein Ereignis im Intervall \(\Delta x = \pm 2 \sigma\) um den Mittelwert \(\mu = 3,00\) mit der Standardabweichung \(\sigma = 0,5\) vorzufinden, wenn die Werteverteilung durch eine Gausssche Verteilungsfunktion beschrieben werden kann?
Lösung:
(D) ist richtig. \(3 - 2 \sigma =2\); \(3+2 \sigma = 4\).
Q3-10 —Standardabweichung einer Messreihe
Gegeben seien Ihnen Messwerte, die um einen Mittelwert streuen: Datenfile. Die Werte liegen als komma-separierte Liste vor und können mittels make dataW={... Werte...} in Igor importiert werden.
Berechnen Sie die Probenstandardabweichung \(\sigma_P\) der Daten auf drei Stellen genau!
(B) ist richtig.
Wir lesen ab: V_sdev \(= \sigma_P\ = 0.52641\).
Q3-11 —z-Wert eines zweifelhaften Datenpunktes
Gegeben seien Ihnen Messwerte, die um einen Mittelwert streuen: Datenfile. Es handelt sich um dieselbe Liste wie in Q43 und Q44. Die Werte liegen als komma-separierte Liste vor.
Eine graphische Darstellung der Messwerte finden Sie hier:
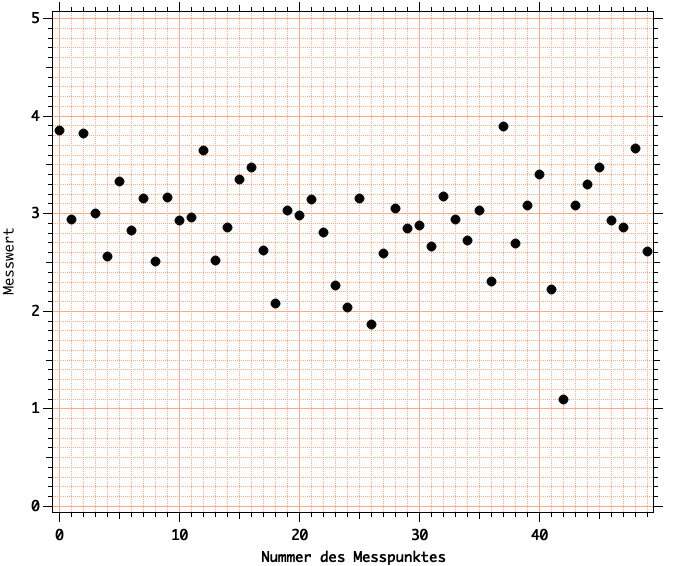
Es fällt auf, dass der Messpunkt mit der Nummer 42 (die Zählung beginnt mit Null) und dem Wert \(1,1\) aus der Reihe tanzt
: er ist deutlich kleiner als alle anderen Werte. Um zu ermitteln, ob es sich hier um einen Ausreißer handelt, bestimmen wir zunächst den z-Wert des Datenpunktes. Nutzen Sie hierzu die Ergebnisse für \(\mu\) und \(\sigma\) aus der Statistik des Datensatzes (wavestats kann hilfreich sein)! Der Wert ist auf drei Stellen zu runden.
(D) ist richtig.
Der \(z\)Wert gibt an, um wieviele Standardeinheiten ein gegebener Wert vom Mittelwert abweicht. Nutzung von wavestats ergibt:
\(\mu = 2,91\) und \(\sigma = 0,526\)
Der fragliche Datenpunkt hat den Wert \(y=1,1\). Er weicht also um einen Betrag von \(1,81\) vom Mittelwert ab. Daraus ergibt sich: \[ z = \frac{\left|x-\mu\right|}{\sigma} = \frac{1,81}{0,526} = 3,44. \]
Der Datenpunkt weicht um 3,44 Standardabweichungen vom Mittelwert ab, und der z-Wert ist daher \(z=3,44\).Q3-12 —Wahrscheinlichkeit für das Auftreten eines Ausreißers
Wir nutzen weiterhin, so wie den Aufgaben Q3-10 und Q3-11 Messwerte, die in folgender Datei verlinkt sind: Datenfile.
Nutzen Sie die Ergebnisse der Aufgaben Q44 und Q45, und berechnen Sie die Wahrscheinlichkeit für das Auftreten des Datenpunktes mit dem Wert1.1. Berechnen Sie hierzu die Wahrscheinlichkeit dafür, dass ein Datenpunkt mindestens \(\pm z\) Standardabweichungen vom Mittelwert \(\mu\) entfernt ist. Formulieren Sie mit den statistischen Daten des Datensatzes für \(\mu\) und \(\sigma\) die Gausssche Verteilungsfunktion für die gegebenen Werte, und ermitteln Sie durch Integration die Wahrscheinlichkeit \(\Delta W\) für ein Auftreten außerhalb des Bereiches \(\left(\mu \pm z\cdot \sigma\right)\). Die Vorgehensweise ist in der 5. Vorlesung genauestens beschrieben.
Lösung:
(B) ist richtig.
In Igor:
Das ergibt \(\Delta W = 0.000581734 = 5.87 \cdot 10^{-4}\). Wie man sieht, bekommt man das in wenigen Schritten heraus.
Q3-13 —Ausreißer (Fortsetzung von Q3-12)
Welche der folgenden Aussagen über die Konsequenzen der Übungsaufgaben Q44 bis Q46 sind richtig?
(A) und (B) sind richtig.
Multiplizieren wir die in Aufgabe Q46 erhaltene Wahrscheinlichkeit von \(P = 5,8 \cdot 10^{-4}\) mit der Zahl \(N\) der Punkte (50 Datenpunkte), dann erhalten wir:
\[ P \cdot 50 = 2,9 \cdot 10^{-2}. \]Das ist natürlich kleiner als \(\tfrac{1}{2}\).
(B) ist richtig, denn das ist ja unser Kriterium für einen Ausreißer.
(C) ist falsch; die Standardabweichung wird kleiner, wenn wir den Punkt weglassen (sie beträgt dann nur noch \(\sigma'= 0,462\).
(D) ist falsch; wenn Sie einen Punkt weglassen, der noch dazu stark streut, dann ändert sich der Mittelwert über die restlichen Daten.