— Brechungsindex

---

Dringt Licht einer gegebenen Wellenlänge aus dem Vakuum unter dem Winkel \(\alpha_{V}\) zum Lot in ein transparentes Medium ein, so ändert sich der Winkel zum Lot auf einen Wert \(\alpha\) (siehe Abbildung). Dieses Phänomen wird als Brechung des Lichtes bezeichnet.

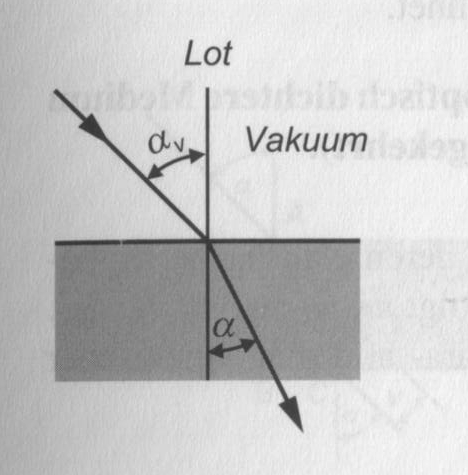Das Verhältnis der beiden Winkel wird als Brechungsindex \(n_{0}\) bezeichnet: \[ \frac{\sin \alpha_{V}}{\sin \alpha} = n_0. \] Wie groß ist der Brechungsindex \(n_{0}\) des Mediums einschließlich des wahrscheinlichsten Fehlers \(\Delta n_{0}\), wenn \(\alpha_{V} = \left(30 \pm 1\right)^{\circ}\) und \(\alpha = \left(21 \pm 1\right)^{\circ}\)?
Hinweis: Rechnen Sie zunächst alle Winkel in \({\rm rad}\) um!

   \(n_0 =\)   

(A)\(1,4 \pm 0,1\) (B)\(1,395 \pm 0,075 \) (C)\(1,40 \pm 0,075\) (D)Keine der Antworten (A) — (C) ist richtig.