
Messen in der Chemie
– Sommersemester 2022
4. Vorlesung (16.05.2022)
Praktisch jeder moderne Messaufbau in der Physikalischen Chemie ist computergestützt (im PC-Praktikum gibt es hiervon Ausnahmen, aber das sind dann keine zeitgemäßen Versuchsaufbauten, vielmehr dienen sie didaktischen Zwecken). Rechner spielen eine zentrale Rolle in verschiedenen Phasen (Abschnitten) eines Experimentes:
Curve Fitting, das spielt eine wichtige Rolle im PC-Praktikum).
Datenanalyse-Software enthält oft umfangreiche Mathematik-Pakete, die eine Auswertung der Messdaten überhaupt erst ermöglichen (Beispiel: Fourier-Transformation von Interferogrammen in der FTIR-Spektroskopie).
Neben Datenanalyse-Programmen gibt es auch reine Mathematik-Programme, die das Leben erheblich erleichtern, weil sie umständliche und fehleranfällige mathematische Prozeduren übernehmen, wie z.B. das Ableiten und Integrieren einer Funktion, oder das Auflösen einer Gleichung nach einer darin auftretenden Größe. Programme, die mit symbolischer Mathematik umgehen können, also z.B. das Ingetral \(\int x^2 \cdot \exp(-x) \diff x\) ausrechnen, oder den Grenzwert von \(\frac{\sin x}{x^2} \) an der Stelle \(x=0\) ermitteln können, werden CAS-Programme (CAS = Computer Algebra System) genannt.
Kommerzielle CAS-Programme können sehr viel Geld kosten. Es gibt aber einige kostenfreie Möglichkeiten, Mathematik am Computer zu betreiben, wenn man es nicht hauptberuflich tut; hier werden nur zwei aufgelistet.
Basic Accountzulegen, erhöht sich die Ihnen täglich zur Verfügung stehende Prozessorzeit.
Für unsere Zwecke sind Numerik-Programme aber viel wichtiger als CAS-Programme. Diese liefern nicht symbolische Lösungen eines Problems, sondern Zahlenwerte, beispielsweise die Fläche unter einer experimentell bestimmten Kurve.
Speziell zur zahlenmäßigen Flächenbestimmung gab es früher die Methode der Chemiker-Integration
: die auf Papier aufgetragene Kurve wurde bis zur Abszisse mit der Schere ausgeschnitten und auf eine Analysenwaage gelegt. Das ist heute nicht mehr zeitgemäß, da die Messdaten ohnehin digital vorliegen und dementsprechend mit einem Programm ausgewertet werden können.
Ein für unsere Zwecke fast immer geeignetes Programm zur Datenerfassung, -auswertung und -darstellung ist die Software Igor Pro des Herstellers WaveMetrics, das zur Nutzung im Rahmen des Praktikums und begleitender Lehrveranstaltungen (also auch Messen in der Chemie
) allen Teilnehmern kostenlos zur Verfügung gestellt wird.
Im Folgenden werden wir mit Igor auf Tuchfühlung gehen; im weiteren Verlauf dieser Lehrveranstaltung werden wir es häufig nutzen.
Wenn Sie das Programm starten, öffnet Igor zwei Fenster: (a) eine Tabelle zum Eintragen von Daten; (b) ein Kommandofenster zum Eingeben und Auflisten von Befehlen (siehe Abb. 4-1).
Schließen Sie bitte das Tabellenfenster, dieses werden wir vorläufig nicht brauchen.

Den lästigen Symbolstreifen (Toolbar
) unter der Titelleiste des Kommandofensters werden Sie los, indem Sie im Menü Windows
auf Hide Toolbar
klicken. Im folgenden wird das Kommandofenster ohne den (die? das?) Toolbar gezeigt.
Unter dem roten Streifen des Kommandofensters ist die eigentliche Befehlszeile. Hier spielt die Musik.
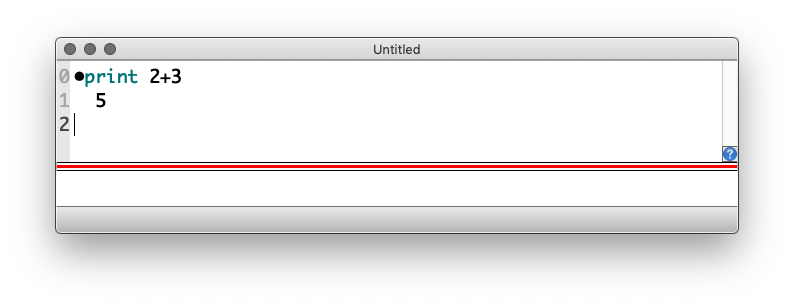
Geben Sie dort bitte ein:
und betätigen Sie die Return-Taste Ihrer Tastatur zum Abschicken des Befehls. Igor macht jetzt folgendes:
History:
Mathematische Funktionen haben die in Computersprachen üblichen Bezeichnungen, so ist zum Beispiel die Quadratwurzel aus 2 durch folgenden Befehl zugänglich:
print sqrt(2)
Das Argument der Wurzelfunktion wird in Klammern hinter das Wurzelzeichen sqrt geschrieben.
Dies gilt ganz allgemein: \(\ln 2\) wird erhalten durch den Befehl ln(2), der Sinus von 1.3 \(\rm rad\) durch sin(1.3).
Damit Ihre Daten nicht verloren gehen, sollten Sie das Projekt jetzt auf Ihrem Rechner abspeichern; dabei kann ein beliebiger Name und ein beliebiger Speicherort verwendet werden. Igor verwendet die Endung pxp
als Dateinamenserweiterung. Das hier gezeigte Igor-Projekt wurde unter dem Namen IgorIntro
abgespeichert; der Name des Projektes erscheint nachfolgend in der Titelleiste des Kommandofensters.
Datentypen.— Wie jede Programmierumgebung verfügt auch Igor über spezielle Datentypen. Wir stellen hier zunächst zwei besonders wichtige vor:
(1) Datentyp variable
: Der elementarste Datentyp heißt variable und entspricht einfach einer Zahl. Geben Sie bitte ein, und bestätigen Sie jeweils mit Return:
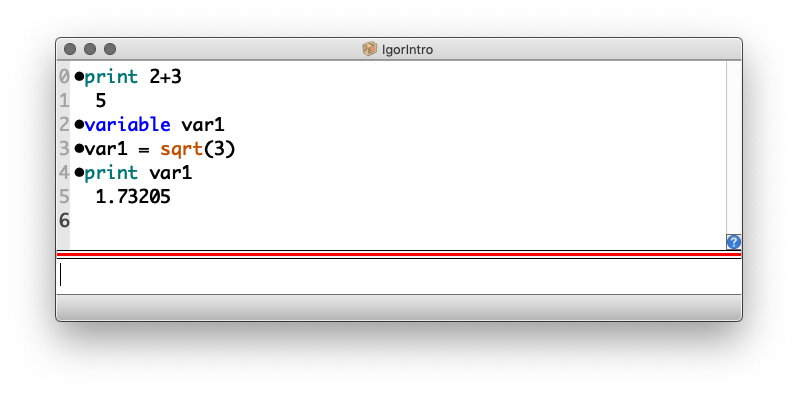
Die Variable var1 existiert nur innerhalb des aktuellen Igor-Projektes (hier also IgorIntro). Wenn Sie ein neues Projekt anfangen, kennt Igor var1 nicht.
(2) Datentyp wave
: Das ist der wichtigste Datentyp. Eine Wave entspricht einer geordneten Liste von Zahlen, also ungefähr dem, was in einem Tabellenkalkulationsprogramm wie MS Excel in einer Spalte der Tabelle dargestellt wird.
Mit »geordnet« ist hier nicht gemeint, dass die Werte nach ihrer Größe oder einem sonstigen Kriterium sortiert sind; sondern dass es auf Reihenfolge der Elemente der Wave ankommt.
Hier ein Gegenbeispiel: Nehmen wir an, Sie haben folgende Einkaufsliste beim Besuch im Supermarkt dabei:
Eier, Mohrrüben, Milch, Müsli.
Hier kommt es auf die Reihenfolge der Liste nicht an. In Ihrer Einkaufstüte würde sich nach dem Verlassen des Ladens dasselbe befinden, wenn auf Ihrem Einkaufszettel statt dessen gestanden hätte:
Milch, Mohrrüben, Eier, Müsli.
Geradeso wie Variablen haben auch Waves stets einen Namen. Zum Erzeugen einer Wave gibt es den Befehl make, wie wir hier an einem Beispiel zeigen:
Die Wave heißt also testW
, die einzelnen Zahlen stehen in geschweiften Klammern dahinter, durch ein Komma separiert. Beachten Sie, dass als Dezimalseparator ein Punkt verwendet wird.
Zur Namensgebung von Variablen und Waves gibt es einige Regeln, die zu beachten sind.
Wenn eine Wave mit dem Namen testW nicht allzu viele Elemente enthält, kann man sie mit dem Befehl print testW in der History ausdrucken.
Das ist alles, was wir im Augenblick brauchen; weitergehende Funktionalität werden wir später kennenlernen. Wir werden im folgenden Abschnitt Igor-Waves benutzen, um an Datensätzen Statistik zu betreiben.
4.3.– Streuung von Messdaten.–
Mittelwert, Varianz, Standardabweichung.
Wiederholte Messungen liefern nicht stets dasselbe Ergebnis. Beispiel: Wir setzen eine Lösung an, die nach einer bestimmten Zeit einem plötzlichen Farbumschlag unterworfen sein soll. Wird dieser Versuch einige Male wiederholt, so unterscheiden sich die Versuchsbedingungen doch jedes Mal geringfügig: die Konzentration der Lösung ist nicht dieselbe, die Temperatur kann geringfügig höher sein, die Helligkeit im Labor ist nicht dieselbe, die Adaptierung der Augen ist etwas anders als zuvor usw. Diese und ähnliche Änderungen in den äußeren Umständen führen zu zufälligen Schwankungen der gemessenen Zeit bis zur Wahrnehmung des Farbumschlags.Aus den Beobachtungen werden Messwerte gewonnen; diese bilden zunächst eine Reihe von Zahlenwerten.
Hier ist ein Beispiel einer solchen Messreihe:
6,86; 6,85; 7,39; 6,98; 8,02; 7,62; 6,30; 6,80; 7,03; 7,80; 7,2; 8,19
Die Messreihe ist eine Liste von Zahlenwerten (die zugeordnete Einheit ist hier ganz belanglos, es könnten also z.B. titrierte Milliliter sein). Für den \( i \)-ten Messwert wollen wir das Symbol \( x_{i} \) verwenden.
Der wichtigste Informationsgehalt einer Messreihe, bei der wiederholt dieselbe Größe gemessen wird, ist ihr Mittelwert \( \mu \).
Es lässt sich theoretisch zeigen, dass der Mittelwert \(\mu\) mit größerer Wahrscheinlichkeit dem wahren Wert entspricht als irgendeiner der Einzelwerte.
In vielen Fällen gibt es aber in der Realität nichts, was einem wahren Wert
entsprechen könnte. Beispiel: wenn wir das Körpergewicht aller Teilnehmer an dieser Lehrveranstaltung messen, entsteht eine Liste aus Zahlenwerten, aber dem Mittelwert entspricht nicht eine reale Person.
Wir haben also insgesamt \(N\) Messpunkte; wir summieren alle Messwerte \(x_i\), also \(x_1\), \(x_2\), \(x_3\) und so weiter, und teilen diese Summe durch die Anzahl \(N\) der Messungen. Unter das Summenzeichen \(\sum\) schreibt man den Startwert der Laufzahl \(i\), also den Index des ersten Messwerts \(x_1\), und über das Summenzeichen die Laufzahl des letzten der \(N\) Messwerte, also \(N\). Der Einfachheit halber lässt man bei der Obergrenze das \(i=\)
gewöhnlich weg und schreibt einfach \(N\), wenn das eindeutig ist. So wollen wir auch im Folgenden verfahren.
Der Mittelwert ist auf den meisten wissenschaftlichen Taschenrechnern als
Funktion vorhanden, das Zeichen dafür ist häufig \( \mu \) oder \( \bar{x} \) (lies: x quer
). Machen Sie sich bitte mit der entsprechenden Funktionalität Ihres Taschenrechners anhand der Betriebsanweisung vertraut.
Eine Liste kann in Igor importiert werden. Eine Liste wird in Igor als Wave repräsentiert, denn eine Wave ist ja zunächst nichts weiter als eine Liste von Zahlenwerten.
Damit wir mit der Liste in Igor bequem arbeiten können, definieren wir sie und geben ihr einen Namen, zum Beispiel L1. Geben Sie also bitte an der nächsten Befehlszeile ein (copy-paste funktioniert):
Bitte beachten Sie:
Die Wave L1 ist jetzt definiert. Igor verfügt über Funktionen, die auf die Liste wirken.
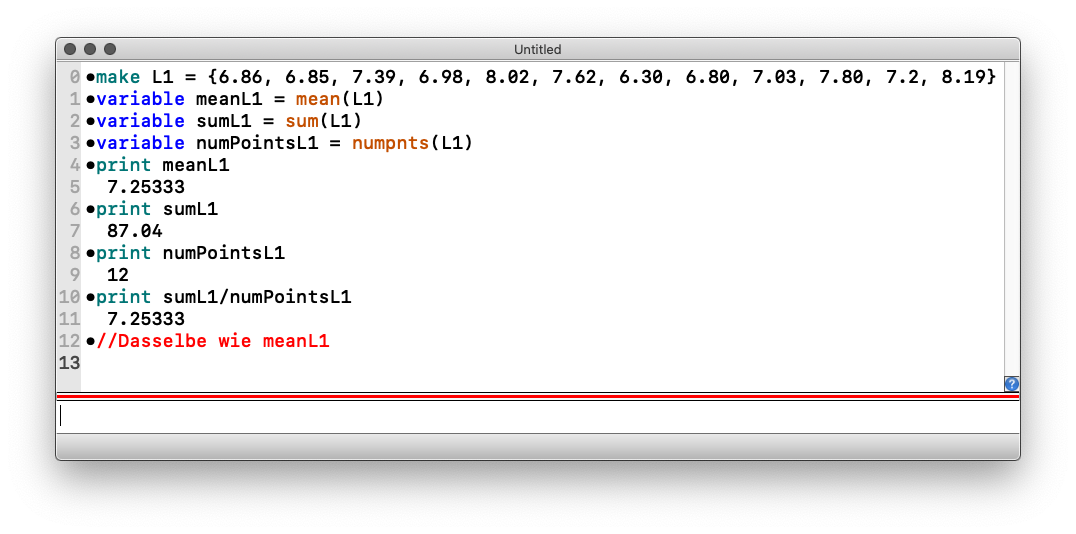
Damit sind wir mit der Bestimmung des Mittelwertes auch schon fertig. In der Abbildung 4 sehen Sie Ein- und Ausgabe im Kommandofenster:
Streuung um den Mittelwert.– Neben dem Mittelwert interessiert uns die Frage, in welchem Ausmaß die Einzelwerte um dieses Mittel schwanken, oder, wie wir lieber sagen, streuen. Wir wollen ja wissen, wie nahe unsere Einzelwerte beim Mittelwert liegen.
Man könnte vielleicht zunächst geneigt sein, analog zur Mittelwertbildung die Schwankung der Werte durch den Mittelwert der Abweichung \(x_i-\mu\) der Einzelwerte vom Mittelwert \(\mu\) der Liste zu definieren, also den Ausdruck \[ \frac{1}{N} \cdot \sum_{i=1}^{N} \left(x_{i}- \mu\right) \] zu verwenden, aber man überzeugt sich leicht, dass dieser Ausdruck stets Null ergibt (das liegt daran, dass die positiven und negativen Abweichungen der Einzelwerte vom Mittelwert sich immer genau kompensieren, probieren Sie es ruhig mit der Liste L1 aus!). Das funktioniert also prinzipiell nicht.
Um die gegenseitige Kompensation der Abweichungen vom Mittelwert zu eliminieren, könnte der Ausdruck \[ \frac{1}{N} \sum_{i=1}^{N} \left|{x_{i}- \mu}\right| \] verwendet werden (also unter Nutzung der Beträge der Abweichungen); aber auch dieser schafft Probleme. Dies ist in der Abb. 5 gezeigt.

Als Maß der Streuung wird häufig die Varianz \( V \) verwendet. Sie ist wie folgt definiert: \begin{equation} \label{eqDefVariance} V = \frac{1}{N} \cdot \sum_{i=1}^{N} \left(x_{i} - \mu \right)^{2.} \end{equation} Beachten Sie das Quadrat in der Summe. Wir summieren also die Quadrate der Abweichungen.
Auch bei der Varianz als Maß der Steubreite treten Probleme auf:
Im PC-Praktikum, und generell in der Physikalischen Chemie, wie die Standardabweichung \( \sigma \) als Maß der Streuung der Einzelwerte verwendet. \(\sigma\) ist definiert als die Quadratwurzel aus der Varianz: \begin{equation} \label{eqDefStdDev} \sigma = \sqrt{V} = \sqrt{ \frac{1}{N} \cdot \sum_{i=1}^{N} \left(x_{i} - \mu \right)^{2} } \end{equation}
Die in Gl. \ref{eqDefStdDev} definierte Größe \( \sigma \) wird auch als Gesamtstandardabweichung bezeichnet. Man muss tiefer in die Urgründe der Statistik einsteigen, um den Hintergrund dieses Begriffes zu verstehen.
Neben dieser Gesamtstandardabweichung \(\sigma\) wird die Probenstandardabweichung \( \sigma_{P} \) verwendet; diese ist definiert als \begin{equation} \label{eqProbenstandardabweichung} \sigma_{P} =\sqrt{ \frac{1}{N-1} \cdot \sum_{i=1}^{N} \left(x_{i} - \mu \right)^{2} } \end{equation}
Sie unterscheidet sich von der in Gl. \ref{eqDefStdDev} definierten Gesamtstandardabweichung (die wir auch als Standardabweichung schlechthin bezeichnen) durch das Auftreten der Größe \(N-1\) statt \(N\) im Nenner vor dem Summenzeichen. Für große \(N\) ist der Unterschied irrelevant. Auf Taschenrechnern ist meist \( \sigma_{P} \) verfügbar (dies muss im Handbuch des Taschenrechners nachgelesen werden).Zur Gesamtstandardabweichung \( \sigma \) entsprechend Gl. \ref{eqDefStdDev} gelangt man, indem man in den Taschenrechner zunächst alle Werte in das Summenregister eingibt, dann den Mittelwert \(\mu\) berechnen lässt, diesen dann ebenfalls in das Summenregister eingibt und erst danach die Standardabweichung vom Taschenrechner mit der entsprechenden Befehlstaste errechnen lässt.
Der Unterschied zwischen der Standardabweichung der Gesamtheit \( \sigma \) und der Standardabweichung der Probe \( \sigma_{P} \) ist fast immer belanglos. Um Dinge nicht allzu kompliziert zu machen, können Sie in der Regel mit demjenigen \( \sigma \) rechnen, das Ihr Computerprogramm bzw. Taschenrechner anbietet, außer es wird ausdrücklich Wert auf den Unterschied gelegt.
Mit der Software Igor können Sie die Standardabweichung der Werte aus der Liste L1 (siehe oben) erhalten. Es gibt aber (meines Wissens zumindest) keinen Befehl, der unmittelbar \(\sigma\) liefern würde. Statt dessen verwenden wir den Befehl wavestats, der eine Fülle von statistischen Informationen über den Datensatz liefert. Führen Sie also den folgenden Befehl aus:
Die Ausgabe sieht dann wie folgt aus:
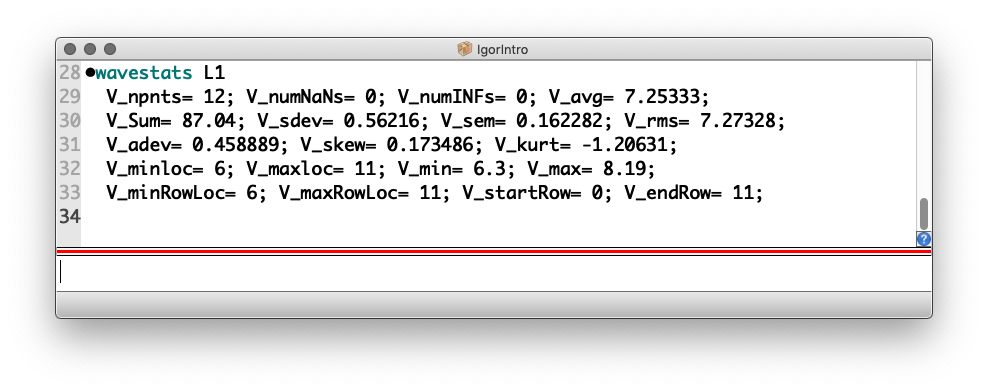
Hier die wichtigsten der erzeugten Variablen (sie beginnen alle mit V_
):
unendlichenthalten; für uns von geringer Bedeutung.
verbessert die Statistik, aber nur im folgenden Sinne:
Der Fehler des Mittelwertes ist nicht dasselbe wie die Standardabweichung. \(\sigma\), die Standardabweichung, gibt an, wie stark Messpunkte um einen Mittelwert streuen. Der Fehler des Mittelwertes, den wir mit \(\Delta \mu\) bezeichnen, gibt an, wie genau der Mittelwert \(\mu\) bekannt ist; wie groß seine Unsicherheit \(\Delta \mu\) ist. \(\Delta \mu\) hängt aber eng mit der Standardabweichung \(\sigma\) zusammen und ist definiert als \begin{equation} \label{eqErrorOfMean} \Delta \mu = \frac{\sigma}{\sqrt{N}}. \end{equation}
Probieren Sie es aus; geben Sie ein:
und Sie erhalten den Zahlenwert von \(\Delta \mu\).
Um den Fehler des Mittelwertes zu erhalten, teilen wir also die Standardabweichung \(\sigma\) nochmals durch die Wurzel aus der Zahl der Messdaten.
Gegeben sei eine Standardabweichung von \(\sigma=3.5\) bei einer Anzahl von 20 Datenpunkten. Der Fehler des Mittelwertes ist dann gegeben zu
\[ \Delta \mu_1 = \frac{3.5}{\sqrt{20}};\] wenn wir aber 40 Messpunkte aufnehmen, so erhalten wir: \[ \Delta \mu_2 = \frac{3.5}{\sqrt{40}}.\] Teilen wir die beiden \(\Delta \mu\)-Werte durcheinander, so finden wir: \[ \frac{\Delta \mu_1}{\Delta \mu_2} = \frac{3,5 \cdot \sqrt{40}}{\sqrt{20}\cdot 3,5} = \frac{\sqrt{40}}{\sqrt{20}} = \sqrt{\frac{40}{20}} = \sqrt{2}.\]Bei der halben Anzahl an Messpunkten (20 statt 40) ist also der Fehler des Mittelwertes \(\Delta \mu\) um den Faktor \(\sqrt{2}\) größer. Um einen zehnfach kleineren Fehler des Mittelwertes \(\Delta \mu\) zu erhalten, müssen wir die Anzahl an Messungen verhunderfachen.
Wenn Sie aus einer Messreihe den Mittelwert und den Fehler des Mittelwertes angeben wollen, so verwenden Sie für den Fehler des Mittelwertes bitte den Ausdruck in der Gl. \ref{eqErrorOfMean}.
Mittelwertbildung fehlerbehafteter Größen.–
Die bisherigen Gleichungen gehen davon aus, dass die Messwerte in statistischer Weise um einen Mittelwert schwanken, und es wurden die üblichen statistischen Methoden verwendet, um einen Mittelwert, die Standardabweichung und den Fehler des Mittelwertes zu ermitteln.Häufig kennen wir aber zusätzlich den individuellen Fehler \(\Delta x_i\) der Messwerte \(x_i\). Wir erhalten z.B. aus verschiedenen Messverfahren eine gewisse Größe mit unterschiedlichem Einzelfehler (es könnte sich z.B. um die Messung einer Naturkonstante mit unterschiedlichen Messmethoden handeln). Hierfür gibt es besondere Vorschriften, die wir hier nicht herleiten, sondern nur mitteilen.
Dabei gelten die folgenden Gleichungen: \begin{equation} \label{eqMittelwertFehlerbehaftet} \mu = \frac{\sum_{i=1}^{N}\frac{x_{i}}{\left(\Delta x_i\right)^{2}}}{{\sum_{i=1}^{N}\frac{1}{\left(\Delta x_i\right)^{2}}}} \end{equation} und \begin{equation} \label{eqFehlerMittelwertFehlerbehaftet} \Delta \mu = \sqrt{\frac{1}{{\sum_{i=1}^{N}\frac{1}{\left(\Delta x_i\right)^{2}}}}}. \end{equation}
Diese Gleichungen gelten auch für den wichtigen Sonderfall, dass alle Fehler \(\Delta x_i\) einander gleich sind.
Die Gleichungen \(\ref{eqMittelwertFehlerbehaftet}\) und \(\ref{eqFehlerMittelwertFehlerbehaftet}\) sehen furchterregend aus, sie können aber mit Hilfe eines Tabellenkalkulationsprogrammes wie MS Excel oder auch mit Igor ohne viel Mühe genutzt werden.
Wir führen hier vor, wie man \(\mu\) und \(\Delta \mu\) in Igor ermittelt; dabei lernen wir gleichzeitig einiges Neue über das Programm kennen.
Die Messdatenreihe weise die folgenden Elemente auf:
{6, 5.8, 6.3, 6.1, 5.9, 6.2, 6.1}
Die Fehler der Einzelmessungen seien wir folgt gegeben:
{0.2, 0.3, 0.2, 0.4, 0.1, 0.1, 0.2}
Zählerwave) gewählt; ein Name ist so gut wie der andere:
Bitte beachten Sie, dass der Fehler des Mittelwertes deutlich kleiner ist als die Einzelfehler!
In der Abb. 4-7 ist die Abfolge der Befehle zu sehen. Es sind nur wenige Zeilen:
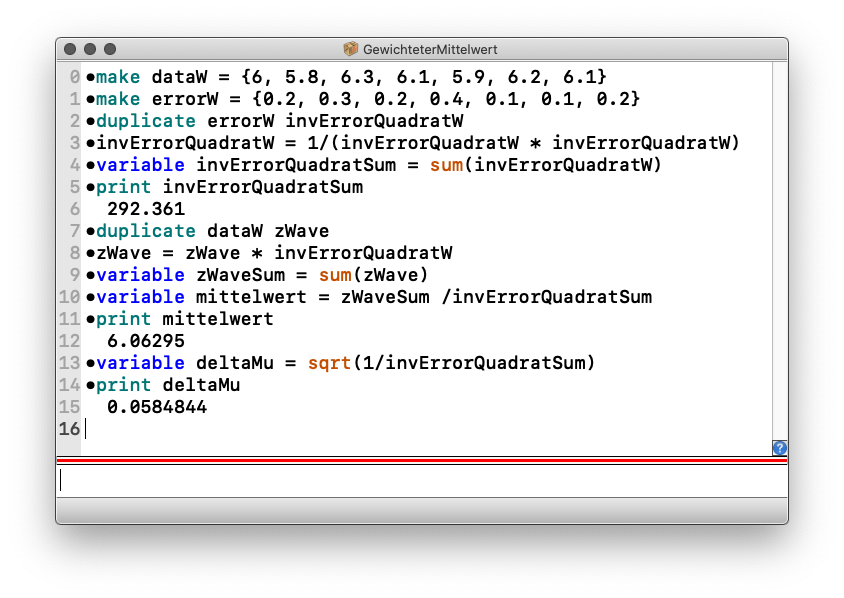
Es sei zugestanden, dass diese Lerneinheit vollgestopft mit unhandlichen Gleichungen ist. Wegen der ständig auftretenden Summenzeichen ist es schwierig, die entsprechenden Rechnungen auf Papier von Hand auszuführen. Mindestens benötigt man einen wissenschaftlichen Taschenrechner. Wenn Sie keinen solchen haben, sollten Sie sich einen zulegen; es gibt sie für unter 20 Euro zu kaufen. Achten Sie beim Kauf darauf, dass der Rechner Statistikfunktionen hat.
Wir wollen zur Erheiterung nun ein Computerspiel machen, das Ihnen einen Eindruck von den Ursachen der Streuung von Messdaten vermitteln kann. Das Spiel heißt Quincunx und zeigt die Verteilung von zufälligen Ereignissen. Hier ist der Link auf Quincunx. Klicken Sie bitte auf den Link, so dass sich ein weiteres Browserfenster öffnet und Sie das Spiel sehen.
So sieht die Spielfläche von Quincunx aus:
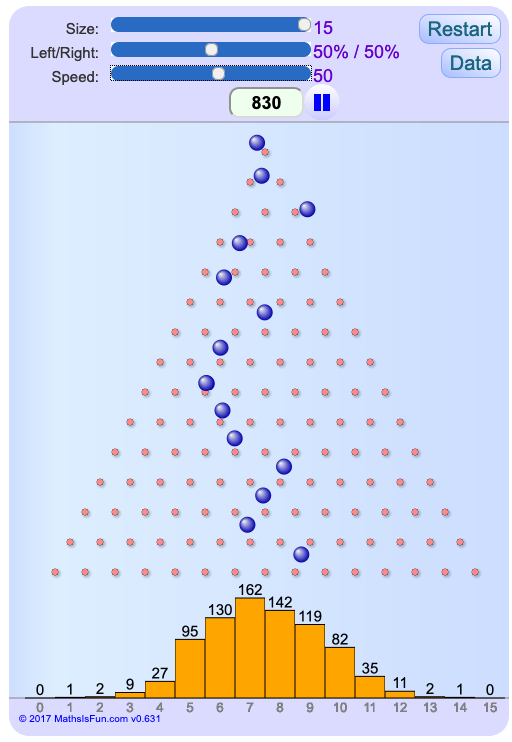
Stellen Sie bitte den Schieberegler Size
auf den Maximalwert (15) und Speed
auf 50. Klicken Sie dann Restart
.
Die blauen Bälle, die nach unten fallen, treffen auf Stangen (die Sie von vorne sehen). Die Wahrscheinlichkeit, dass ein Ball links an der Stange entlang fällt, ist gerade so groß, wie dass er rechts daran herabfällt. So hüpft jeder Ball beim Fallen immer zwischen Stangen hin und her. Unten im Bild sehen die die Häufigkeiten, mit denen die Bälle schließlich in den einzelnen Bereichen unter den Stangen auftreffen. Sie werden feststellen, dass die meisten Bälle nahe der Mitte des Feldes landen, aber eben nicht alle Bälle. Einige treffen auch weit entfernt von der Mitte auf. Da die Verteilung rein zufällig ist, werden Sie bei einer Wiederholung des Spieles während einer gleich langen Zeit nicht wieder genau dieselbe Verteilung erhalten, sondern nur eine ihr ähnliche.
Bitte lassen Sie nach Möglichkeit das Spiel über Nacht laufen. Im Laufe der Zeit wird die Verteilung der Bälle auf die zur Verfügung stehenden Plätze immer regelmäßiger. Dahinter steckt eine strenge Gesetzmäßigkeit, die man Binomialverteilung nennt.
In der nächsten Lerneinheit werden wir diese Verteilung genauer unter die Lupe nehmen. Wir werden herausfinden, was geschieht, wenn wir die Zahl der Auftreffplätze unendlich groß machen (jedes Intervall also unendlich klein), und auch die Zahl der Bälle unendlich groß werden lassen. Dabei ergibt sich eine mathematische Funktion mit faszinierenden Eigenschaften, die wir mit Igor untersuchen werden. Dabei werden wir Igor auch als Graphik-Maschine kennenlernen. Wir werden lernen, dass es diese Funktion ist, die den Schlüssel zu dem Formelsalat liefert, den wir bisher im Rahmen der Fehlerrechnung besprochen haben. Lassen Sie sich überraschen, bleiben Sie (im Wortsinn!) am Ball, und die nächste Teillieferung kommt in einer Woche!
Danke für die Lektüre!
R.F.